Opération algébrique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Nyarlathotep
- Membre Naturel
- Messages: 80
- Enregistré le: 15 Nov 2008, 14:09
-
 par Nyarlathotep » 08 Sep 2009, 17:27
par Nyarlathotep » 08 Sep 2009, 17:27
bonjour, petite question:
est ce que je peux écrire: 4^n+2=3k <=> 4^n=3k-2 <=> n=3k-2/4
merci d'avance!
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 08 Sep 2009, 17:32
par uztop » 08 Sep 2009, 17:32
Salut,
non tu ne peux pas,

Sinon, tu devrais utiliser latex pour rendre les formules plus lisibles (ou au moins mettre des parentheses)
-
Nyarlathotep
- Membre Naturel
- Messages: 80
- Enregistré le: 15 Nov 2008, 14:09
-
 par Nyarlathotep » 08 Sep 2009, 17:36
par Nyarlathotep » 08 Sep 2009, 17:36
d'accord, mais comment je pourrais simplifier l'équation 4^n=3k-2??

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 08 Sep 2009, 17:41
par Ericovitchi » 08 Sep 2009, 17:41
en prenant le log népérien à droite et à gauche.
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 08 Sep 2009, 17:41
par uztop » 08 Sep 2009, 17:41
ton expression de départ est

ou

?
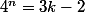
ne peut pas vraiment se simplifier, tu peux écrire
}{ln4})
si tu veux mais c'est tout.
-
Nyarlathotep
- Membre Naturel
- Messages: 80
- Enregistré le: 15 Nov 2008, 14:09
-
 par Nyarlathotep » 08 Sep 2009, 17:43
par Nyarlathotep » 08 Sep 2009, 17:43
d'accord mais je n'ai pas encore vu les logarithmes népériens^^, mais je dois me tromper quelque part.
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 08 Sep 2009, 17:45
par uztop » 08 Sep 2009, 17:45
le seul moyen de se débarasser des puissances est d'utiliser les ln (qu'on voit en terminale); donc si tu as des puissances dans ton expression, il doit effectivement y avoir une erreur quelque part :)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Sep 2009, 16:54
par Nightmare » 09 Sep 2009, 16:54
Salut.
Remarque que
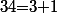
Par conséquent
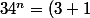^{n}=1+\Bigsum_{k=1}^{n} C_{n}^{k} 3^{n-k})
(binôme de Newton).
On vérifiera facilement que la somme est divisible par 3.
Si tu ne connais pas le binôme de Newton, une autre méthode est la récurrence :
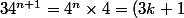*4 = 3(4k+1)+1)
qui est bien divisible par 3, je te laisse vérifier que la propriété est vraie au rang initial n=1.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
