Bonsoir tout le monde!
Je suis nouvelle sur ce forum qui m'a été présenté par martin :lol4:
Je suis en terminale ES, mon professeur de mathématiques nous donne régulièrement des d.m. à faire, c'est bien ça nous entraîne mais pour le dernier il a oublié une chose...de nous donner le cours pour faire le d.m.! :doh:
Donc je bloque totalement :soupir2:
Je vais vous montrer un morceau de l'énoncé, si vous pouviez me donner les cours pour que je puisse le faire et comprendre les logarithmes, ce serait génial :++:
Partie A:
On considère la fonction g définie sur ]1; + l'infini[ par :
g (x) = ax+ b/ ln x
Déterminer les réels a et b pour que la représentation graphique (T) de g dans (O ; i ; j) coupe l'axe (O ; i) au point E d'abscisse e et que la tangente à (T) en E soit parallèle à la droite d'équation y = 2x .
(ln désigne le logarithme népérien et e le nombre réel tel que ln e = 1).
Le ln me bloque tout, j'ai tapé l'équation dans ma calculatrice, ça "merdouille", je n'ai aucune idée de ce que je peux faire, je me sens "bête" lol :marteau:
Je vous remercie d'avance de votre aide qui me sera précieuse et d'une grande utilité :++:
Nouvelle et déjà des problèmes lol : logarithmes
4 messages
- Page 1 sur 1
salut, te donner un cours n'est pas evident ,tu peux regarder ici :
http://xmaths.free.fr/TS/cours/cours.php?nomcours=TSlncours&page=01
sinon pour to exo.
}=ax+\frac{b}{ln(x)})
on te dit que:
equation de l'axe) c'est y=0 donc si on traduit l'nnoncé ça equivaut à g(e)=0 soit:
c'est y=0 donc si on traduit l'nnoncé ça equivaut à g(e)=0 soit:
}=0)
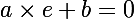 (1)
(1)
on te dit ensuite que:
equation de la tangente au point d'abscisse est donnée par:
est donnée par:
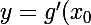(x-x_0)+g(x_0))
donc le coefficient directeur de la tangente est)
ici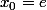 donc il faut que
donc il faut que=2)
on calcule=a-\frac{b}{x(ln(x))^2})
soit=a-\frac{b}{e})
donc
=2)
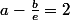 (2)
(2)
(1) et (2) forment un systeme d'equation de 2 equations à 2 inconnues qu'il te faut resoudre afin de trouver a et b
http://xmaths.free.fr/TS/cours/cours.php?nomcours=TSlncours&page=01
sinon pour to exo.
Déterminer les réels a et b pour que la représentation graphique (T) de g dans (O ; i ; j) coupe l'axe (O ; i) au point E d'abscisse e et que la tangente à (T) en E soit parallèle à la droite d'équation y = 2x .
(ln désigne le logarithme népérien et e le nombre réel tel que ln e = 1).
on te dit que:
la représentation graphique (T) de g dans (O ; i ; j) coupe l'axe (O ; i) au point E d'abscisse e
equation de l'axe
on te dit ensuite que:
or deux droites sont paralleles ssi elles ont même coefficient directeurla tangente à (T) en E soit parallèle à la droite d'équation y = 2x .
equation de la tangente au point d'abscisse
donc le coefficient directeur de la tangente est
ici
on calcule
soit
donc
(1) et (2) forment un systeme d'equation de 2 equations à 2 inconnues qu'il te faut resoudre afin de trouver a et b
Bonjour,
Merci pour votre aide.
Donc si je ne me suis pas trompée :
{ a x e + b = 0
{ a - b/e = 2
<=> (2+b/e) x e +b = 0
a = 2 + b/e
<=> 2e +b +b = 0
a = 2 + b/e
<=> 2e + 2b = 0
a = 2 + b/e
<=> 2b = 0- 2e
a = 2 + b/e
<=> b = - e
a = 2 + -e/e
<=> b = -e
a = 2 + (-1) = 1
Est-ce correct? :girl2:
Est-ce tout ce qu'il faut faire pour cette première partie?
Merci pour votre aide.
Donc si je ne me suis pas trompée :
{ a x e + b = 0
{ a - b/e = 2
<=> (2+b/e) x e +b = 0
a = 2 + b/e
<=> 2e +b +b = 0
a = 2 + b/e
<=> 2e + 2b = 0
a = 2 + b/e
<=> 2b = 0- 2e
a = 2 + b/e
<=> b = - e
a = 2 + -e/e
<=> b = -e
a = 2 + (-1) = 1
Est-ce correct? :girl2:
Est-ce tout ce qu'il faut faire pour cette première partie?
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
