I^2 = -1 ? On nous aurait menti ?
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
fhfhfufss
- Membre Naturel
- Messages: 39
- Enregistré le: 28 Juil 2015, 15:05
-
 par fhfhfufss » 22 Aoû 2015, 15:27
par fhfhfufss » 22 Aoû 2015, 15:27
Carpate a écrit:Tu ne lis pas attentivement ce que j'écris et de plus, dans ce que tu écris, différent de ce que j'ai écrit :
)
tu introduis S sans nous l'avoir présenté !
Qui est ce monsieur ou cette dame ?
Question programme je ne suis pas compétent, les années lycée remontant à quelques 4 décennies !
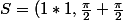)
En gros ce qui me pose problème c'est pas S mais
)
. Pourquoi faire
)
z1*z2= (r1;a1)*(r2;a2)=(r2r1;a1+a2) d'après ce que tu m'as dis...
Donc que viens faire :
)
dans ton expression pour le calcul de la valeur de i^2...
Les quote par d'elle même :
Carpate a écrit:\
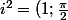 (1;\frac{\pi}{2}) = (1,\frac{\pi}{2}+\frac{\pi}{2})(1;\pi)= -1)

-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 22 Aoû 2015, 15:38
par Carpate » 22 Aoû 2015, 15:38
fhfhfufss a écrit: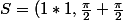)
En gros ce qui me pose problème c'est pas S mais
)
. Pourquoi faire
)
z1*z2= (r1;a1)*(r2;a2)=(r2r1;a1+a2) d'après ce que tu m'as dis...
Donc que viens faire :
)
dans ton expression pour le calcul de la valeur de i^2
Restons calmes.
Partons de la définition du produit de 2 complexes. Si tu ne l'a pas encore vu en cours, il te faudra l'admettre.
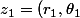)
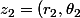)
leur produit est, par définition du produit de 2 complexes le complexe dont le module est le produit des modules et un argument la somme des arguments
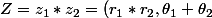)
Appliqué au complexe
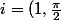)
:
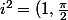*(1,\frac{\pi}{2})=(1*1,\frac{\pi}{2}+\frac{\pi}{2})=(1,\pi)=cos(\pi)+i*sin(\pi)=-1)
-
fhfhfufss
- Membre Naturel
- Messages: 39
- Enregistré le: 28 Juil 2015, 15:05
-
 par fhfhfufss » 22 Aoû 2015, 15:59
par fhfhfufss » 22 Aoû 2015, 15:59
Carpate a écrit:Restons calmes.
Partons de la définition du produit de 2 complexes. Si tu ne l'a pas encore vu en cours, il te faudra l'admettre.
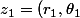)
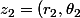)
leur produit est, par définition du produit de 2 complexes le complexe dont le module est le produit des modules et un argument la somme des arguments
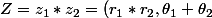)
Appliqué au complexe
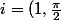)
:
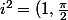*(1,\frac{\pi}{2})=(1*1,\frac{\pi}{2}+\frac{\pi}{2})=(1,\pi)=cos(\pi)+i*sin(\pi)=-1)
Ok merci j'ai compris

.
Par contre je ne vois toujours pas pourquoi le produit de deux complexe est le "produit est, par définition du produit de 2 complexes le complexe dont le module est le produit des modules et un argument la somme des arguments".
T'aurais pas une explication ?
-
fhfhfufss
- Membre Naturel
- Messages: 39
- Enregistré le: 28 Juil 2015, 15:05
-
 par fhfhfufss » 22 Aoû 2015, 16:06
par fhfhfufss » 22 Aoû 2015, 16:06
Je crois que j'ai une idée :
comme
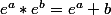
Les arguments s'ajoutent. Ce qui ne me convint toujours pas car pour être franc je n'est pas compris pourquoi
) = z = |z|*(cos(arg(z))+isin(arg(z))))
On a peut être fait la démo durant l'année mais sans vraiment insister dessus je vais réfléchir sur ça déjà.
Par contre pourquoi multiplier les modules ; je ne sais pas....
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 22 Aoû 2015, 16:08
par Carpate » 22 Aoû 2015, 16:08
fhfhfufss a écrit:Ok merci j'ai compris

.
Par contre je ne vois toujours pas pourquoi le produit de deux complexe est le "produit est, par définition du produit de 2 complexes le complexe dont le module est le produit des modules et un argument la somme des arguments".
T'aurais pas une explication ?
Et si tu te décidais à consulter un cours sur les complexes, au hasard :
https://fr.wikiversity.org/wiki/Calcul_avec_les_nombres_complexes/Module_et_argument
-
fhfhfufss
- Membre Naturel
- Messages: 39
- Enregistré le: 28 Juil 2015, 15:05
-
 par fhfhfufss » 22 Aoû 2015, 16:11
par fhfhfufss » 22 Aoû 2015, 16:11
dans ton cours : |z|=|-z| ; ce n'est pas possible car un module est positif non ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 22 Aoû 2015, 16:19
par Carpate » 22 Aoû 2015, 16:19
fhfhfufss a écrit:dans ton cours : |z|=|-z| ; ce n'est pas possible car un module est positif non ?
D'abord ce n'est pas mon cours !
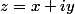
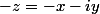
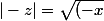^2+(-y)^2} = \sqrt{x^2+y^2}=|z|)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
