fhfhfufss a écrit:Merci pour ton aide je commence à y voir plus clair...
J'aurais encore besoin de précisions :
1. Dans mon cours il est écris qu'une image est un point et pas un vecteur...
2. Pourquoi alors quand on place l'image de l'affixe z=a+ib on place b selon l'axe des ordonnés et a selon l'axe des abscisses ?
3. Pourquoi multiplies-tu ensuite par
)
si multiplier de complexes c'est ajouter leur argument et multiplier leur module ?
4. Enfin j'ai toujours du mal a comprendre pourquoi
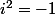
malgré ton explication. En effet, je ne vois pas trop ce que c'est, géométriquement ; que de multiplier des points.... Ok on multiplie leur affixe mais
pourquoi ?
C'est pas dans mon cours je viens de vérifier :mur:
Cordialement,
1) Je fais un copier-coller d'un cours (pris au hasard)
Affixe - image Soit (x, y)  R 2 .
R 2 .
Laffixe du point M de coordonnées (x, y) est le complexe z M = x + iy.
Laffixe du vecteur u de coordonnées (x, y) est le complexe z u = x + iy.
Limage du complexe de forme algébrique z = x + iy est le point M (x, y).
Le vecteur image du complexe de forme algébrique z = x + iy est le vecteur u(x, y).Effectivement on parle d'image pour un complexe (c'est donc un point)
et de vecteur-image pour un vecteur u(x,y) dont on connaît l'affixe z = x+iy
2) parce que dans la forme algébrique z=a+ib, a est par définition la partie réelle de z donc est portée par l'axe des abscisses (axe des réels) et b la partie imaginaire et est portée par l'axe des ordonnées (axe des imaginaires)
3)
Dans : (1;\pi)= -1) je n'avais pas écrit 1*1 pensant que c'était évident
je n'avais pas écrit 1*1 pensant que c'était évident4) on ne multiple pas des points mais des nombres complexes
Quand on multiple i par lui-même, on applique le complexe i au complexe i dont le vecteur image est le vecteur unitaire de l'axe des ordonnées.
Or multiplier par i c'est appliquer la rotation
)
au vecteur image on obtient donc un vecteur dirigé selon l'axe des abscisses et de sens opposé à son vecteur unitaire soit le vecteur(-1,0) dont l'affixe est le complexe
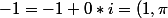=e^{i\pi})
J'arrive pas à croire que l'on ne définit pas le produit de 2 complexes dans ton cours !

