Notion de tangente

par **Anonyme** » 05 Déc 2009, 15:16

Bonjour

Alors voila je m'interroge sur la definition d'une tangente a une courbe.
Selon mon prof la tangente est une droite qui coupe une courbe en deux point presque confondu donc une secante particuliere. Wikipedia semble dire la meme chose. (je croyais que la tangente coupait la droite en un point ...)

Donc selon la definition: dans un repere orthonorme l'axe des abscisses coupes la represenation graphique de la fonction

en deux point pourtant en effectuant des calculs on trouve qu'un seul point O(0,0).

Or je trouve la une contradiction pas vous ?
(Ici j'ai pris comme exemple la fonction

avec l'axe des abscisse juste pour donner un exemple et pour ne pas rester dans l'abstrait mais on retrouve cette "contradiction" partout ou il y a des tangentes)

Merci

par **Le_chat** » 05 Déc 2009, 15:20

Non, il n'y a pas vraiment de contradiction. La tangente est une droite qui passe bien par 2 points de la courbe, mais en faisant tendre la distance entre ces deux points vers 0.

par **Billball** » 05 Déc 2009, 15:21

l'animation de la partie " Définition géométrique de la tangente" le représente bien pourtant ou revoir la définition du nombre dérivée :

f'(a) = lim f(x) - f(a) / (x - a) x-> a

par **Anonyme** » 05 Déc 2009, 15:29

Vous etes d'accords avec moi que

est une tangente a la courbe

?

Si oui alors calculons les points d'intersection:
Il suffit de resoudre

==>

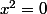
Je vois un seul point ...

par **Le_chat** » 05 Déc 2009, 15:32

Mais la tangente coupe ta courbe en 1 seul point... je ne vois pas le problème.
Tu prends le point O (0,0), et tu en prends un autre sur la courbe:M (x,x^2).
Tu calcules l'equation de OM et hop, tu fais tendre M vers O... plus qu'un seul point.

par **Anonyme** » 05 Déc 2009, 15:42

Le_chat a écrit:Mais la tangente coupe ta courbe en 1 seul point... je ne vois pas le problème.

Justement il est la le probleme elle devrait couper la courbe en deux point presque confondu donc deux points pas un point ...

par **Le_chat** » 05 Déc 2009, 15:47

Sauf que tu fais se rapprocher tes points, ils en deviennent infiniment proches.
Donc on peut dire qu'ils sont confondus (il reste bien 2 points, mais infiniment proches). En gros, si on appelle d la distance OM, on veut que pour tout e>0, d;)e.

par **Billball** » 05 Déc 2009, 15:47

Le_chat a écrit:Mais la tangente coupe ta courbe en 1 seul point... je ne vois pas le problème.
Tu prends le point O (0,0), et tu en prends un autre sur la courbe:M (x,x^2).
Tu calcules l'equation de OM et hop, tu fais tendre M vers O... plus qu'un seul point.

c'est pour ça qu'il y a 2 points .. faut faire tendre vers l'infiniment petit jusqu'a en avoir qu'un

par **Anonyme** » 05 Déc 2009, 15:49

Vous etes d'accords qu'il y a deux points certes infiniment proches mais deux points ? Et que aussi infiniment qu'ils soient proches il y aura toujours deux points non confondus ?

par **Ben314** » 05 Déc 2009, 15:50

Tes calculs sont justes : la tangente ne coupe qu'en UN point.
Le fait de dire qu'elle coupe en "deux points presque confondus" est une image pour ce représenter l'idée de tangente.
par exemple quelle serait l'équation d'une droite passant par (0,0) et "presque" horizontale ? Combien de points d'intersection y aurait il ?

P.S. il n'y a pas "deux" points mais un seul.

par **Anonyme** » 05 Déc 2009, 15:52

Ben314 a écrit:Tes calculs sont justes : la tangente ne coupe qu'en UN point.
Le fait de dire qu'elle coupe en "deux points presque confondus" est une image pour ce représenter l'idée de tangente.
par exemple quelle serait l'équation d'une droite passant par (0,0) et "presque" horizontale ? Combien de points d'intersection y aurait il ?

un point

Ben314 a écrit:P.S. il n'y a pas "deux" points mais un seul.

J'ai pourtant verifier les definition et il y a deux points

par **Le_chat** » 05 Déc 2009, 15:56

Ptete un truc plus parlant:
On prend O, et on choisi M tel que d(O,M)=1/n. tu fais tendre n vers l'infini, et hop, d(O,M)=0.

par **Ben314** » 05 Déc 2009, 15:57

Si on veut préciser un peu plus cette notion de "deux points" en mathématique, voici quelques petites remarques :
Normalement , une équation de la forme (x-a)(x-b)=0 a (évidement) 2 solutions : x=a et x=b.
Que se passe t'il si a=b ? (x-a)(x-a)=0 n'a (évidement) plus qu'une seule solution x=a. Souvent, pour préciser que le (x-a) apparait deux fois, on dit que cette solution est une "solution double".
Pour revenir à ton problème, quad tu cherche l'intersection de la courbe y=x^2 et de sa tangente en (0,0), cela revient à résoudre x^2=0.
La SEULE solution est bien x=0, mais c'est une "solution double".

Tu peut essayer avec d'autre courbes et d'autres tangentes : on a toujours une "solution double" et on peut interpréter cela comme si cela signifiat que l'on a deux solutions.... au même endroit.

par **Ben314** » 05 Déc 2009, 15:58

Qmath a écrit:J'ai pourtant verifier les definition et il y a deux points

Peut tu me donner cette définition s.t.p.

par **Anonyme** » 05 Déc 2009, 16:03

Donc (x'x) coupe y = x^2 en deux points confondu ...
Mais alors pourquoi dit-on que (x'x) la coupe en un seul point ? C'est une erreur mathematique non ?

par **Le_chat** » 05 Déc 2009, 16:05

Bah franchement, je vois plus de grande différence entre 2 points confondus et un point. A la limite, elle coupe xx' en 17 points confondus...

par **Anonyme** » 05 Déc 2009, 16:06

Ben314 a écrit:Peut tu me donner cette définition s.t.p.

Deja la definition de mon premier post vient de mon prof de maths et je trouve qu'elle rejoint cela:

Wiki a écrit:la tangente à une courbe en un de ses points est une droite qui « touche » la courbe au plus près au voisinage de ce point.

par **Anonyme** » 05 Déc 2009, 16:14

Apres moi je ne fais que repeter la definition de mon prof qui pourrait se tromper alors j'aimerais que quelqu'un me definisse rigoureusement ce que c'est une tangente a une courbe et qu'il m'explique cette ambigüité qu'il y a (en combien de points la tangente coupe la courbe)

Merci

par **Ben314** » 05 Déc 2009, 16:36

D'abord une petite précision :
Il est parfaitement possible qu'une tangente coupe la courbe 36 fois (connais tu la courbe de la fonction sinus ?).

Aprés, il y a plusieurs définition possible de la tangente à une courbe C en un point M de la courbe : en voici quelques unes :

1) La tangente est la droite passant par M qui "reste du mème coté" de la courbe autour du point M (cette définition a des inconvénients....)

2) La tangente, c'est la droite que l'on obtient lorsque l'on trace la droite (MN) où N est un autre point de la courbe puis que l'on prend N de plus en plus proche de M (ca c'est une BONNE définition)

3) La tangente c'est la droite passant par M telle que, quand on résoud l'équation pour trouver l'intersection avec la courbe on ait une "solution double".

Il faut faire attention avec le mot "solution double" : dans ton exemple (y=x^2 et la tangente en 0), il n'y a bien qu'UN SEUL point d'intersection et pas 2 et l'équation x^2=0 n'a bien qu'UNE SEULE solution. Par contre, comme x^2=(x-0)(x-0) on dit que la solution est "double" cela ne veut pas dire du tout qu'il y a deux solutions.

par **Ben314** » 05 Déc 2009, 16:39

L'idée des "solutions doubles" c'est que par exemple l'équation
(x-2)(x-2)=0 n'a qu'une solution mais, si le la change "à peine" en mettant à la place (x-2)(x-1.99999)=0, elle se met à avoir 2 solution.

Dans ton exemple, cela signifie que, si on bouge "à peine" la tangente, elle se met à couper 2 fois.
Mais, (j'insiste) si on ne la bouge pas elle ne coupe qu'UNE fois.

Notion de tangente

Notion de tangente

Qui est en ligne