hey, bonjour a toi qui lis ce petit message !
j'avais une question à poser, après avoir refait tout mon cour sur les dérivations, je ne comprend toujours pas comment faire la différence entre trouver le domaine de définition dune fonction f et justifier sa dérivibalité.
bon voila si quelqu'un pourrait m'expliquer ( je sais ça a l'ère tout bête) MERCIII
Notion de dérivé
3 messages
- Page 1 sur 1
Re: notion de dérivé
Bonjour,
Le domaine de définition, ou ensemble de définition selon les uns et les autres, c'est l'ensemble des nombres pour lesquels la fonction est définie.
Par exemple, si on dit que f est une fonction de [0;1] dans R, alors le domaine de définition c'est [0;1], même si la formule est calculable ailleurs.
Si on donne la formule et qu'on demande "quel est le domaine de définition", alors il faut examiner :
La dérivabilité, c'est l'ensemble des nombres pour lesquels la fonction admet un nombre dérivé. Le nombre dérivé, c'est d'abord un nombre réel, limite du taux de variation, c'est-à-dire
-f(x)}{h}})
Il y a donc deux conditions : que la limite existe, d'une part, et qu'elle ne soit pas infinie, d'autre part.
EXEMPLE
La fonction racine carrée :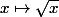
Le domaine de définition est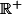 (la variable doit être positive ou nulle)
(la variable doit être positive ou nulle)
Mais la fonction n'est dérivable que sur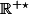 ; en effet, pour x=0, on a
; en effet, pour x=0, on a
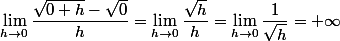
Limite infinie, donc non dérivable en 0.
Le domaine de définition, ou ensemble de définition selon les uns et les autres, c'est l'ensemble des nombres pour lesquels la fonction est définie.
Par exemple, si on dit que f est une fonction de [0;1] dans R, alors le domaine de définition c'est [0;1], même si la formule est calculable ailleurs.
Si on donne la formule et qu'on demande "quel est le domaine de définition", alors il faut examiner :
- les dénominateurs des fractions (qui ne doivent pas être nuls)
- le contenu des radicaux (racine carrée), qui doivent être positifs ou nuls
- les contenus des logarithmes, qui doivent être strictement positifs
La dérivabilité, c'est l'ensemble des nombres pour lesquels la fonction admet un nombre dérivé. Le nombre dérivé, c'est d'abord un nombre réel, limite du taux de variation, c'est-à-dire
Il y a donc deux conditions : que la limite existe, d'une part, et qu'elle ne soit pas infinie, d'autre part.
EXEMPLE
La fonction racine carrée :
Le domaine de définition est
Mais la fonction n'est dérivable que sur
Limite infinie, donc non dérivable en 0.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: notion de dérivé
ajoutons qu'il existe des fonctions définies, continues sur R et dérivables en aucun point (elle n'ont pas de dérivée). Leurs courbes présentent des rugosités, des picots , en tout point qui rendent impossible le passage à la limite de leur taux de variation.
En l'espèce, on a=R) et
et =\emptyset) (ensemble vide)
(ensemble vide)
En l'espèce, on a
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
