Nombres premiers entre eux

[mehdi-128]

Bonjour,

Soit p un entier naturel supérieur ou égal à 1.

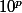
1/ Montrer que et sont premiers entre eux.
J'ai réussi avec le théorème de Bezout.

2/ En déduire que p est supérieur ou égal à 2 et est premier avec

Je bloque pour la 2.

Merci

[Arbre]

Bonjour,

Sans plus d'info sur p tu ne peux rien dire.

Prends par exemple p=1 alors tu as bien 10 et 9 premier.
Mais p est plus petit que 2.

Prends maitenant p=10 le point 1/ reste toujours vrai.
Mais p n'est pas premier avec 2^j5^k.

[pascal16]

l'énoncé n'est pas complet, la question 2 ne rime à rien.
(10^p) - 1 peut être ?

[zygomatique]

de toute façon il n’arrête pas de donner des bouts d'énoncé sans queue ni tête ...

[mehdi-128]

l'énoncé n'est pas complet, la question 2 ne rime à rien.
(10^p) - 1 peut être ?

Oui c'est ça c'est pourquoi on a :

[mehdi-128]

de toute façon il n’arrête pas de donner des bouts d'énoncé sans queue ni tête ...

En effet mais j'y peux rien c'est la fin d'un long problème du CAPES 2014 et c'est difficile de tout résumé sans oublier de choses.

[zygomatique]

alors tout simplement nous le préciser et nous donner un lien ...

[aymanemaysae]

Bonjour ;

Le lien de l'énoncé est : http://www.maths-france.fr/Capes/Capes_ ... Enonce.pdf ,

et le lien du corrigé est : http://www.maths-france.fr/Capes/Capes_ ... orrige.pdf ,

mais je ne vois pas le lien avec les questions de Mehdi-128 .

[mehdi-128]

Bonjour ;

Le lien de l'énoncé est : http://www.maths-france.fr/Capes/Capes_ ... Enonce.pdf ,

et le lien du corrigé est : http://www.maths-france.fr/Capes/Capes_ ... orrige.pdf ,

mais je ne vois pas le lien avec les questions de Mehdi-128 .

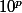
Je comprends pas la partie du corrigé page 10 lorsqu'il dit : et sont premiers entre eux donc et 10^p -1 n'admet ni 2 ni 5 comme facteur premier et est donc premier avec même si j=k=0.
Comment on sait que 10^p -1 sera premier avec ?

[Pseuda]

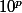
Je comprends pas la partie du corrigé page 10 lorsqu'il dit : et sont premiers entre eux donc et 10^p -1 n'admet ni 2 ni 5 comme facteur premier et est donc premier avec même si j=k=0.
Comment on sait que 10^p -1 sera premier avec ?

Bonsoir,

Eh bien parce que tout nombre entier (même 0) est premier avec 1 (ils n'admettent que 1 comme diviseur commun, il suffit de revenir à la définition de "nombres premiers entre eux").

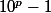
car ne peut être égal ni à 0 ni à 1 d'après ce qui précède.

[mehdi-128]

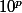
Je comprends pas la partie du corrigé page 10 lorsqu'il dit : et sont premiers entre eux donc et 10^p -1 n'admet ni 2 ni 5 comme facteur premier et est donc premier avec même si j=k=0.
Comment on sait que 10^p -1 sera premier avec ?

Bonsoir,

Eh bien parce que tout nombre entier (même 0) est premier avec 1 (ils n'admettent que 1 comme diviseur commun, il suffit de revenir à la définition de "nombres premiers entre eux").

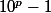
car ne peut être égal ni à 0 ni à 1 d'après ce qui précède.

Ah merci j'ai enfin compris