[Résolu] Nombres Complexes - Techniques
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 25 Aoû 2007, 17:57
par Melkor » 25 Aoû 2007, 17:57
Bonjour à tous, j'ai un exercice sur les complexes, pas très compliqué mais plutôt "encombrant"..., enfin vous comprendrez en lisant la suite :
Écrire sous formes algébriques les complexes suivant :
A=(1+i)^44 B=((racine de 3)/3 + i/6)^18
Développer est réalisable à l'aide du triangle de Pascal, cependant, je voudrais savoir si il n'existe pas une technique pour que ce soit moins encombrant, car sur ma feuille, je manque de place ! :lol2:
Merci de votre aide...
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 25 Aoû 2007, 18:04
par anima » 25 Aoû 2007, 18:04
Melkor a écrit:Bonjour à tous, j'ai un exercice sur les complexes, pas très compliqué mais plutôt "encombrant"..., enfin vous comprendrez en lisant la suite :
Développer est réalisable à l'aide du triangle de Pascal, cependant, je voudrais savoir si il n'existe pas une technique pour que ce soit moins encombrant, car sur ma feuille, je manque de place ! :lol2:
Merci de votre aide...
Passer en forme polaire ou expo et utiliser la formule de moivre me semble parfait

^{44} = (\sqrt{2}(cos(\frac{\pi}{4})+isin(\frac{\pi}{4})))^{44} \\<br />= [\sqrt{2};\frac{\pi}{4}]^{44} \\<br />= [(\sqrt{2})^{44};11\pi] \\<br />= [2^{22};\pi])
sauf erreur.
^18)
T'es sur que c'est pas rac(3)/6?

-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 25 Aoû 2007, 18:06
par kazeriahm » 25 Aoû 2007, 18:06
salut
1+i=sqrt(2)*exp(iPi/4), pareil pour l'autre
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 25 Aoû 2007, 18:09
par Melkor » 25 Aoû 2007, 18:09
anima a écrit:Passer en forme polaire ou expo et utiliser la formule de moivre me semble parfait

^{44} = (\sqrt{2}(cos(\frac{\pi}{4})+isin(\frac{\pi}{4})))^{44} \\<br />= [\sqrt{2};\frac{\pi}{4}]^{44} \\<br />= [(\sqrt{2})^{44};11\pi] \\<br />= [2^{22};\pi])
sauf erreur.
^18)
T'es sur que c'est pas rac(3)/6?

Oui, c'est bien
^18)
Par contre je comprends pas
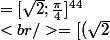^{44};11\pi] \\<br />= [2^{22};\pi])
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 25 Aoû 2007, 18:17
par anima » 25 Aoû 2007, 18:17
Melkor a écrit:Oui, c'est bien
^18)
Par contre je comprends pas
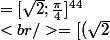^{44};11\pi] \\<br />= [2^{22};\pi])
N'as-tu jamais vu cette formule:
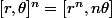
? :doh:
Sinon, pour l'autre....je reflechis. Il faudrait factoriser par le module (racine de 13 sur 6)
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 25 Aoû 2007, 18:19
par Melkor » 25 Aoû 2007, 18:19
anima a écrit:N'as-tu jamais vu cette formule:
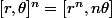
? :doh:
Sinon, pour l'autre....je reflechis. Il faudrait factoriser par le module (racine de 13 sur 6)
je ne pense pas avoir vu cette formule, aussi loin que remonte mes souvenirs, je ne sais même pas ce que c'est, car à mon avis les crochet ont une signification précise
surtout que pour écrire sous forme algébrique je ne vois pas comment ça peut m'aider, vu qu'il faut que ce soit de la forme : a+bi
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 25 Aoû 2007, 18:21
par anima » 25 Aoû 2007, 18:21
Melkor a écrit:je ne pense pas avoir vu cette formule, aussi loin que remonte mes souvenirs, je ne sais même pas ce que c'est, car à mon avis les crochet ont une signification précise
Forme polaire d'un complexe;
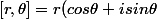)
:we:
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 25 Aoû 2007, 18:29
par Melkor » 25 Aoû 2007, 18:29
anima a écrit:Forme polaire d'un complexe;
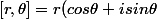)
:we:
je connais
)
mais l'autre je sais pas
après c'est sur ça peut aider pour calculer le complexe à la puissance 44 d'après ta formule, j'ai [4 194 304 ;11pi]
ça voudrait alors dire que mon complexe s'écrit 4 194 304(cos(11pi)+isin(11pi))?
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 25 Aoû 2007, 18:30
par anima » 25 Aoû 2007, 18:30
Melkor a écrit:je connais
)
mais l'autre je sais pas
après c'est sur ça peut aider pour calculer le complexe à la puissance 44 d'après ta formule, j'ai [4 194 304 ;11pi]
ça voudrait alors dire que mon complexe s'écrit 4 194 304(cos(11pi)+isin(11pi))?
Voui. Tu peux verifier si tu veux; ma Ti92+ me dit que (1+i)^44 = -4194304, soit 4194304(-1), or,
cos(11pi)=-1; sin(11pi)=0
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 25 Aoû 2007, 18:34
par Melkor » 25 Aoû 2007, 18:34
anima a écrit:Voui. Tu peux verifier si tu veux; ma Ti92+ me dit que (1+i)^44 = -4194304, soit 4194304(-1), or, cos(11pi)=-1; sin(11pi)=0
oui c'est logique vu que cos 11pi = cos pi [2pi]
merci pour cette technique que je ne connaissais pas, après pour l'autre faut réussir à la mettre sous forme trigonométrique. Je vais essayer ça.
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 25 Aoû 2007, 19:03
par anima » 25 Aoû 2007, 19:03
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 25 Aoû 2007, 19:09
par Melkor » 25 Aoû 2007, 19:09
anima a écrit: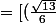^{18};18sin^{-1}\frac{1}{\sqrt{13}}])
est la reponse que je donnerais.
c'est ce que je trouve, sauf que le problème c'est pour trouver l'angle en valeur exact :-/
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 25 Aoû 2007, 19:09
par anima » 25 Aoû 2007, 19:09
Melkor a écrit:c'est ce que je trouve, sauf que le problème c'est pour trouver l'angle en valeur exact :-/
Y'a pas moyen, tu peux approcher, mais tu ne l'auras jamais. C'est comme ca :hum:
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 25 Aoû 2007, 20:05
par Melkor » 25 Aoû 2007, 20:05
Dommage, en tout cas merci de ton aide :++:
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 26 Aoû 2007, 16:47
par Melkor » 26 Aoû 2007, 16:47
Bon je reouvre le topic...
Déterminer sous forme algébrique la racine carrée de :
-2-2i
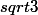
j'ai essayé avec la méthode d'anima, ce qui fait que je me retrouve avec :
)^0,5)
Donc cos
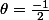
Et sin
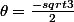
Et là, ben y'a pas d'angle commun :mur:
Si quelqu'un pourrait m'aider là dessus...
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 26 Aoû 2007, 16:50
par anima » 26 Aoû 2007, 16:50
Melkor a écrit:)^18)
Tu te retrouves avec ca? Oh mon dieu, l'angle est
evident:
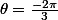
car
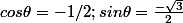
.
De la, on peut dire que
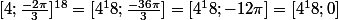
Mais, si on te demande la racine carree de

... C'est pas a la puissance 1/2 plutot? :hum:
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 26 Aoû 2007, 16:55
par Melkor » 26 Aoû 2007, 16:55
anima a écrit:Tu te retrouves avec ca? Oh mon dieu, l'angle est
evident:
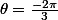
car
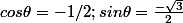
.
De la, on peut dire que
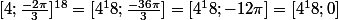
Mais, si on te demande la racine carree de

... C'est pas a la puissance 1/2 plutot? :hum:
oui j'ai corrigé ^^'
c'est bizarre pour le
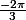
j'ai essayé avec ma calculatrice pour vérifier ça et je trouvais pas le même sinus, j'ai du faire une erreur de frappe
:doh:
bon ben plus de problème alors, merci
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Aoû 2007, 16:56
par yos » 26 Aoû 2007, 16:56
Melkor a écrit:...sous forme algébrique...
^2=-2-2i\sqrt3\Leftrightarrow a^2+b^2=4, a^2-b^2=-2, 2ab=-2\sqrt3 \Leftrightarrow a^2=1, b^2=3, ab<0)
etc.
-
Melkor
- Membre Naturel
- Messages: 80
- Enregistré le: 06 Jan 2007, 20:01
-
 par Melkor » 26 Aoû 2007, 16:58
par Melkor » 26 Aoû 2007, 16:58
yos a écrit:^2=-2-2i\sqrt3\Leftrightarrow a^2+b^2=4, a^2-b^2=-2, 2ab=-2\sqrt3 \Leftrightarrow a^2=1, b^2=3, ab<0)
etc.
Merci pour cette méthode là, je vais l'essayer pour ceux que je ne peux pas faire avec des valeurs exactes

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
