Nombres complexes

[obonnet]

Bonjour,

C'est mon premier post sur ce forum. Je suis un père de famille de 43 ans, donc bien loin du lycée et à peu près inculte en matière de mathématiques.

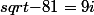
Ce matin, mon jeune garçon m'a affirmé que , me parlant de nombres complexes (dont j'ignorais jusqu'à présent l'existence).

Quelqu'un peut-il s'il vous plaît me confirmer la validité de cette égalité ? Accessoirement, pouvez-vous m'indiquer à quel niveau d'étude correspond ce domaine des mathématiques ?

Je voudrais éviter de laisser le cas échéant mon fils acquérir par lui-même des bases erronées. Merci d'avance pour vos réponses.

[zaze_le_gaz]

c'est vrai

niveau premiere sti, stl

[johnjohnjohn]

Bonjour,


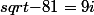
Ce matin, mon jeune garçon m'a affirmé que , me parlant de nombres complexes (dont j'ignorais jusqu'à présent l'existence).

Pour ma part j'ai 42 ans et je ne suis pas prof de maths loin s'en faut. Je continue pour le plaisir à faire des mathématiques. Un étudiant en mathématiques qui lira cette discussion pourra te présenter les choses de façon différente encore :

Ton fils n'a pas tout à fait tort mais pas tout à fait raison non plus. La notation employée est une vraie horreur, néanmoins il y a bien des objets mathématiques dont le carré vaut 81.

Partons de l'équation z²=-81. Dans l'ensemble des réels, il n'y a pas de solutions. Maintenant considérons l'objet i appartenant à l'ensemble des complexes et qui est tel que i²=-1. Ton équation s'écrit désormais :

z²=81.i² ce qui équivaut à z²-81.i²=0 connaissant l'identité remarquable a²-b²=(a-b)(a+b), cette équation équivaut à

(z-9.i)(z+9.i)=0 elle est vérifiée si et seulement si z=9.i ou z=-9.i. On peut donc dire que -81 a deux racines complexes -9.i et +9.i

Pour approfondir :

http://fr.wikipedia.org/wiki/Nombre_complexe

[obonnet]

Merci à tous les deux.

Johnjohnjohn, je vais lui faire part de cette remarque et je suis sûr que ça va beaucoup l'intéresser.

J'ai jusqu'à présent choisi de le tenir éloigné d'Internet vu son jeune âge, mais je pense qu'il gagnerait beaucoup à se former par l'intermédiaire de sites comme celui-ci. Je suis en effet incapable de contrôler moi-même la validité de ses acquis et de ses raisonnements.

[Ben314]

Bonjour,
Etant prof. de math (personne n'est parfait), je voulais (si besoin était) entièrement cautionnner tout ce qu'a écrit johnjohnjohn et préciser (si besoin était aussi) le sens de sa phrase : "pas tout à fait tort mais pas tout à fait raison non plus" :
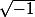
Au début de l'histoire des nombres complexe, les mathématitiens écrivaient sans problème ou mais cela était assez ambigüe du fait qu'il existe DEUX complexe dont le carré donne -81 (voir la preuve de johnjohnjohn)
Depuis un certain nombre d'années, cette écriture avec des racines négatives à été "bannie" du domaine des "choses acceptables" (et, principalement, dans le domaine scolaire)

[obonnet]

Merci pour cette précision Ben314.
Quelqu'un connait-il un livre de vulgarisation mathématiques traitant plus précisément des nombres complexes ?

[Ben314]

Je ne connais pas de livre de vulgarisation sur ce sujet (mais ca doit exister).
Si tu n'est pas alergique au fait de passer du temps devans un écran, tu peut consulter wikipédia (pour l'historique, il y a surement des choses, pour le coté débutant, c'est moin sûr).
Sinon tu peut toujour taper "les complexes pour les nuls" :zen: ou équivalent sous google : je suis persuadé qu'aprés quelques clics tu trouvera chaussure à ton pied (i.e. du niveau qui te va le mieux).