Nombres complexes

[woodis]

Bonjour,
j'ai beaucoup de mal à résoudre certaines questions de cet exercice.
(n),(n+1), ou encore (0,1,2,3...) : sont en indice.
Énoncé :
Dans le plan complexe muni d'un repère orthonormal direct ( O;u;v), on considere les points M(n)= (1/2i)^n(1+ iracine3) ou n est un entier naturel.

1~ exprimez z(n+1) en fonction de z(n), puis znen fonction de z(0) et n. Donnez z(1,2,3,4) sous forme algébrique et sous forme trigonométrique.

2~ Placez les pts M(0,1,2,3,4).

3~ déterminez la distance OM(n) en fonction de n.

4~ a) démontrez que M(n)M(n+1)= (5)/2n pour tout entier naturel n.
b) on pose L(n)= n(symbole de la somme, sorte de E)k=0 M(k) M(k+1).
déterminez L(n) en fonction de n, puis la limite de L(n).

Réponses :

1~ z n+1= (1/2i)^(n+1) (1+i3)
z0= 1+iracine3
Je n'arrive a trouver ni la forme algébrique, ni la forme trigonométrique.

2~ Pour placer les points, il faut que je me serve de la forme algébrique z=a+ib.

3~ Je connais la formule de cours AB = | zb-za|= racine [(xb-xa)²+(yb-ya)²].

4~ Je ne sais pas comment faire.

Aidez-moi s'il vous plait.

[XENSECP]

oula c'est illisible !
utilise TEX

Pour les indices : a_{b} entouré de balise TEX ca te donnera

[woodis]

Merci pour le conseil.

Énoncé :
Dans le plan complexe muni d'un repère orthonormal direct ( O;u;v), on considere les points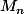 = (1/2i)^n(1+ iracine3) ou n est un entier naturel.

1~ exprimez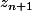 en fonction de 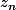, puis 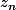en fonction de 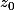et n. Donnez sous forme algébrique et sous forme trigonométrique.

2~ Placez les pts .

3~ déterminez la distance en fonction de n.

4~ a) démontrez que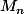 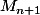= (5)/2n pour tout entier naturel n.
b) on pose = n(symbole de la somme, sorte de E)k=0 .
déterminez en fonction de n, puis la limite de .

Réponses :

1~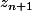 = (1/2i)^(n+1) (1+iracine3)
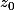= 1+iracine3
Je n'arrive a trouver ni la forme algébrique, ni la forme trigonométrique.

2~ Pour placer les points, il faut que je me serve de la forme algébrique z=a+ib.

3~ Je connais la formule de cours AB = | zb-za|= racine [(xb-xa)²+(yb-ya)²].

4~ Je ne sais pas comment faire.

Aidez-moi s'il vous plait.

[XENSECP]

Tu n'as pas exprimer en fonction de pour la première question
T'as pas réussi les premiers