Nombres complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
buly
- Membre Naturel
- Messages: 12
- Enregistré le: 03 Jan 2007, 22:04
-
 par buly » 04 Jan 2007, 15:37
par buly » 04 Jan 2007, 15:37
[CENTER]Bonjour, je dois faire un exercice sur les nombres complexes, mais je n'ai pas pu suivre la leçon à cause de soucis de santé. Résultat je bloque un peu.
Pourriez vous m'indiquer si mes résultats sont juste et me donner un petit coup de pour pour me débloquer ?
MERCI D AVANCE !
Ps: Je n'arrive pas à effectuer la bonne mise en page alors Z en gras
signifie "le conjugué de Z" (celui qui a une barre au dessus )[/CENTER]
Au point M d'affixe Z=x+iy (avec x différent de y), on fait correspondre le point M' d'affixe :
f(Z)=(Z+Z-i ) / (Z - iZ)
Calculer f(i), en déduire l'écriture trigonométrique de f(i).
Je trouve alors f(i)= (2x-i) / i( x/i +y -x +y/i )
-
Purrace
- Membre Rationnel
- Messages: 536
- Enregistré le: 10 Déc 2006, 16:06
-
 par Purrace » 04 Jan 2007, 15:44
par Purrace » 04 Jan 2007, 15:44
Comment as tu fait pour trouver cela?
Calculer f(i) c'est calculer l'image M' du point M d'affixe z=i par f.
-
buly
- Membre Naturel
- Messages: 12
- Enregistré le: 03 Jan 2007, 22:04
-
 par buly » 04 Jan 2007, 15:47
par buly » 04 Jan 2007, 15:47
Purrace a écrit:Comment as tu fait pour trouver cela?
Calculer f(i) c'est calculer l'image M' du point M d'affixe z=i par f.
Pour faire ce calcul j'ai développé f(Z) en remplaçant Z par x+iy et
Z par x-iy puis j'ai remplacé les x par i
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 04 Jan 2007, 15:47
par allomomo » 04 Jan 2007, 15:47
Salut,
=\frac{2z-i}{z-iz})
=\frac{2i-i}{i-1}=\frac{i}{i-1}=... = \frac{1}{2}-i\frac{1}{2}=\frac{\sqrt{2}}{2}e^{-i\frac{\pi}{4}}=\frac{\sqrt{2}}{2}(cos(\pi/4)-isin(\pi/4)))
(voir repère)
------- Méthode
A chaque fois que tu as
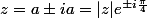
-
buly
- Membre Naturel
- Messages: 12
- Enregistré le: 03 Jan 2007, 22:04
-
 par buly » 04 Jan 2007, 15:51
par buly » 04 Jan 2007, 15:51
allomomo a écrit:Salut,
=\frac{2z-i}{z-iz})
=\frac{2i-i}{i-1}=\frac{i}{i-1}=... = \frac{1}{2}-i\frac{1}{2}=\frac{\sqrt{2}}{2}e^{-i\frac{\pi}{4}})
mais comment fait on pour trouver cela ? :hein:
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 04 Jan 2007, 15:53
par allomomo » 04 Jan 2007, 15:53
Qu'est ce qui ne va pas ?
Si c'est bien ta fonction f, si oui
alors je pense pas qu'il n y ait des erreurs ...
Pose tes questions ...
-
buly
- Membre Naturel
- Messages: 12
- Enregistré le: 03 Jan 2007, 22:04
-
 par buly » 04 Jan 2007, 15:56
par buly » 04 Jan 2007, 15:56
[quote="allomomo"]
=\frac{2z-i}{z-iz})
QUOTE]
Commençons par le commencement, comment as tu réussi à trouver cela ?
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 04 Jan 2007, 15:59
par allomomo » 04 Jan 2007, 15:59
ca c'est ta fonction non ?
-
Purrace
- Membre Rationnel
- Messages: 536
- Enregistré le: 10 Déc 2006, 16:06
-
 par Purrace » 04 Jan 2007, 16:00
par Purrace » 04 Jan 2007, 16:00
Comme je te l'ai dit calculer f(i) c'est calculer l'image du complexe Z=i , tu n'a alors qu'a remplacer Z par i dans ton expression.
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 04 Jan 2007, 16:01
par allomomo » 04 Jan 2007, 16:01
ah je vois
je n'ai pas pris le conjugué en gras (je viens de lire attends je le fait )
-
buly
- Membre Naturel
- Messages: 12
- Enregistré le: 03 Jan 2007, 22:04
-
 par buly » 04 Jan 2007, 16:01
par buly » 04 Jan 2007, 16:01
allomomo a écrit:ca c'est ta fonction non ?
Ma fonction c'est f(Z)= (Z+"conjugué de Z"-i) / ( Z-i"conjugué de Z")
-
buly
- Membre Naturel
- Messages: 12
- Enregistré le: 03 Jan 2007, 22:04
-
 par buly » 04 Jan 2007, 16:03
par buly » 04 Jan 2007, 16:03
Purrace a écrit:Comme je te l'ai dit calculer f(i) c'est calculer l'image du complexe Z=i , tu n'a alors qu'a remplacer Z par i dans ton expression.
Mais pour le "conjugué de i" comment fait on, ça n'existe pas ??
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 04 Jan 2007, 16:07
par allomomo » 04 Jan 2007, 16:07
Re -
Je reprends
=\frac{z+\overline{z}-i}{z-i\overline{z}})
#############################
Ca va changer un peu de ce que j'ai trouvé
#############################
Or
=\frac{i+\overline{i}-i}{i-i\overline{i}}=\frac{-i}{i+1}=...=-\frac{1}{2}+i\frac{1}{2}=\frac{\sqrt{2}}{2}exp(i \frac{3\pi}{4}))
-
buly
- Membre Naturel
- Messages: 12
- Enregistré le: 03 Jan 2007, 22:04
-
 par buly » 04 Jan 2007, 16:09
par buly » 04 Jan 2007, 16:09
mais comment on fait pour le conjugué de i ?
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 04 Jan 2007, 16:14
par allomomo » 04 Jan 2007, 16:14
Le conjugué de i c'est -i ... Voir le cercle trigo
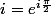
et
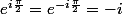
-
buly
- Membre Naturel
- Messages: 12
- Enregistré le: 03 Jan 2007, 22:04
-
 par buly » 04 Jan 2007, 16:19
par buly » 04 Jan 2007, 16:19
MERCI BEAUCOUP ! cette formule était effectivement dans mon cours, mais il n'était pas indiqué qu'il s'agissait de la forme conjuguée
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 04 Jan 2007, 16:23
par allomomo » 04 Jan 2007, 16:23
Un conseil :
Il faut savoir voir, tout est sur le cercle trigo (presque...)
-
buly
- Membre Naturel
- Messages: 12
- Enregistré le: 03 Jan 2007, 22:04
-
 par buly » 04 Jan 2007, 16:57
par buly » 04 Jan 2007, 16:57
au risque que tu n'en puisses plus de mes question je n'arrive pas à passer au calcul que tu as écrit après les "..."
promis je ne t'embete plus après
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 04 Jan 2007, 18:18
par allomomo » 04 Jan 2007, 18:18
J'ai répondu à ton message .... (privé)
C'est la quantité conjuguée
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
