Nombres complexes - passage forme exponentielle

[paulo95]

Bonjour,

Je suis confronté à un petit problème avec les nombres complexes.
Je voudrais passer en forme exponentielle le nombre complexe suivant originellement en forme cartésienne afin d'en calculer les racines : 2i - sqrt(3)

Mon problème est que je ne vois pas comment recupérer la valeur de l'angle.
En effet le module vaut sqrt(7) mais ne permet pas de tomber sur des valeurs remarquable dont on peut convertir les valeurs en angle.


En espérant m'être assez clairement exprimé, je vous remercie d'avance pour vos reponses.

Cordialement

paulo95

[mathelot]

la calculatrice indique
degrés

je te laisse gérer le sgn(x)<0 avec un petit schéma

[Pisigma]

Bonjour,

Il n'est pas obligatoire de trouver une valeur remarquable.

[paulo95]

Merci les gars pour votre réponse rapide.

Malheureusement, je n'ai pas vu les arctan en cours. Y a-t-il une autre solution?

Oui je sais que l'angle n'est pas forcément remarquable mais comment donc le déterminer à ce moment la?

Merci encore pour votre aide :)

[mathelot]

en fait, en relisant ton énoncé, tu veux calculer les "racines carrées" dudit complexe ?
et pour ce faire, on le passe en coordonnées polaires ? je pose la question
car le cas échéant, on peut tout écrire en coordonnées cartésiennes

[paulo95]

oui exactement mathelot , je cherche les racines carrées et cubique de "2i -sqrt(3)" en passant soit par les coordonnées polaires soit exponentielles.

S'il y a un moyen d'y parvenir par la forme cartésienne, je suis preneur, cela peut pourrait aussi convenir.

[mathelot]

oui exactement mathelot , je cherche les racines carrées et cubique de "2i -sqrt(3)" en passant soit par les coordonnées polaires soit exponentielles.

S'il y a un moyen d'y parvenir par la forme cartésienne, je suis preneur, cela peut pourrait aussi convenir.

on cherche une inconnue telle que




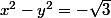
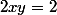
( x et y de même signe)

[paulo95]

Parfait, je te remercie Mathelot.