[TermS] Nombres complexes et géométrie
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
pikmin
- Membre Naturel
- Messages: 94
- Enregistré le: 14 Sep 2005, 16:13
-
 par pikmin » 31 Déc 2006, 01:08
par pikmin » 31 Déc 2006, 01:08
Bonjour,
J'ai un problème sur un exercice de maths que je n'arrive pas à résoudre. Voici l'intitulé :
Le plan complexe est rapporté à un repère orthonormal direct (O, u, v). On considère les points A et B d'affixes respectives i et -i. A tout point M du plan d'affixe z distincte de -i, on associe le point M' d'affixe z' tel que :
z'=(1+iz)/(z+i)
Les premières questions me demandaient de trouver l'image de O, l'antécédent de C d'affixe 1+i et de calculer les solutions de l'équation (1+iz)/(z+i)=z
Ensuite on me demande de vérifier que z'=i(z-i)/(z+i) et d'en déduire que OM'=AM/BM et que (u,OM')=(MB,MA)+PI/2+2kPI et c'est cette dernière question que je n'arrive pas à résoudre (elle concerne les vecteurs)
Merci d'avance pour votre aide
-
pikmin
- Membre Naturel
- Messages: 94
- Enregistré le: 14 Sep 2005, 16:13
-
 par pikmin » 31 Déc 2006, 17:56
par pikmin » 31 Déc 2006, 17:56
toujours personne :cry:
demain ou après-demain j'essarai de mieux formuler ma demande si je n'ai toujours pas de réponse
-
mary123
- Membre Relatif
- Messages: 237
- Enregistré le: 25 Nov 2006, 22:45
-
 par mary123 » 31 Déc 2006, 18:17
par mary123 » 31 Déc 2006, 18:17
pikmin a écrit:
Ensuite on me demande de vérifier que z'=i(z-i)/(z+i) et d'en déduire que OM'=AM/BM et que (u,OM')=(MB,MA)+PI/2+2kPI et c'est cette dernière question que je n'arrive pas à résoudre (elle concerne les vecteurs)
OM'=|z'|=
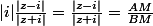
=arg(z')=arg(i\frac{z-i}{z+i})=arg(i)+arg(\frac{z-i}{z+i}))
or
=\frac{\pi}{2})
et
=(MB;MA))
d'ou ton résultat
-
pikmin
- Membre Naturel
- Messages: 94
- Enregistré le: 14 Sep 2005, 16:13
-
 par pikmin » 31 Déc 2006, 18:54
par pikmin » 31 Déc 2006, 18:54
j'ai lu les grandes lignes pour le moment et je pense avoir compris, quand j'aurais le temps je le ferais pour voir si tout est bon, ce qui sera normalement le cas :we:
Merci beaucoup mary :happy2:
-
Purrace
- Membre Rationnel
- Messages: 536
- Enregistré le: 10 Déc 2006, 16:06
-
 par Purrace » 31 Déc 2006, 20:00
par Purrace » 31 Déc 2006, 20:00
La premiere ligne est bonne, mais la suite est fausse arg(z')=arg(i(z-i)/(z+i)) et non pas des modules
-
mary123
- Membre Relatif
- Messages: 237
- Enregistré le: 25 Nov 2006, 22:45
-
 par mary123 » 31 Déc 2006, 20:47
par mary123 » 31 Déc 2006, 20:47
:doh: Oui en effet erreur de copier coller je me rectifie
OM'=|z'|=
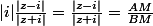
=arg(z')=arg(i\frac{z-i}{z+i})=arg(i)+arg(\frac{z-i}{z+i}))
or
=\frac{\pi}{2})
et
=(MB;MA))
d'ou ton résultat
-
pikmin
- Membre Naturel
- Messages: 94
- Enregistré le: 14 Sep 2005, 16:13
-
 par pikmin » 03 Jan 2007, 16:57
par pikmin » 03 Jan 2007, 16:57
C'est bon j'ai compris, j'ai réussi à finir l'exercie du coup, merci beaucoup :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
