enoncé : Soit

un triangle et
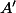
,
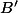
,
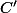
milieux respectifs de
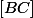
,

,
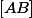
. h est le complexe défini par
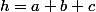
ou

,

,

sont les affixes respectifs des points

,

et

.

est affixe de

.

est le centre du cercle circonscrit au triangle ABC
j'ai démontré dans la question 1 que

est orthocentre du triangle

en utilisant le repère d'origine

.
Dans la question qui me gêne , on pose
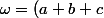/2=h/2)
, affixe du point

et on designe par le point d'affixe et par D le cercle de centre

et de rayon R/2 , soit U(u) milieu de [AH]
--> montrer que
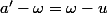
puis en déduire que A' et U appartiennent au cercle D et que |A'U] est diamètre de D.
--> Montrer alors que le pied de la hauteur issue de A sur (BC) appartient à D
J'ai demandé a mon prof il me dit de m'interresser à a' et u par rapport a a,b,c mais cela ne m'aide pas beaucoup ....
J'ai beau retourner cette question dans tous les sens je ne parvient pas a trouver la moindre piste est-ce que quelqu'un pourrait m'aider ?
merci d'avance
