Nombre non multiple de 5 ,carré parfait

[Françoisdesantilles]

Bonjour à tous ,je voulais savoir si quelqu'un pouvais corrigé l'exercice 139 que je n'ai pas compris svp?
J'ai pas compris l'énoncé.

Pour le 136 j'ai écrit des choses, je pense que 5p+4 et 5p-1 ça revient au même .
L'exo 11 n'a rien de prioritaire, je vais revoir comment faire un arbre pondéré .

voici les exo :
https://ibb.co/RYq8ZPp

[Françoisdesantilles]

Voici mes réponses (au brouillon désolé):

https://ibb.co/8zDch90

[Ben314]

Salut,
Pour le 136, c'est O.K.
Ton histoire de "de la forme 5p+4 donc 5p+1", tu peut aussi le rédiger en écrivant simplement que
Tu pouvait aussi un peu alléger le nombre de cas en écrivant qu'un entier non multiple de 5, non seulement on peut l'écrire 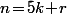avec 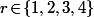, mais aussi sous la forme 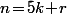avec 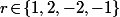ce qui, au signe prés, ne fait que deux cas de figure (et comme on élève au carré, les signes disparaissent).

Pour l'exercice 139, il faut faire la même chose que pour le 136 mais en regardant le reste de la division par 8 du carré d'un entier quelconque (en considérant deux cas selon que l'entier est pair ou impair).
Ensuite, il faut regarder si en ajoutant 3 tels restes (de division par 8 d'un carré) est-ce qu'il est possible d'obtenir 7 (la réponse est "non").
Par contre, je vois pas vraiment l'intérêt de la question 1) qui risque d'embrouiller plus qu'autre chose.

[Françoisdesantilles]

Salut,
Pour le 136, c'est O.K.
Ton histoire de "de la forme 5p+4 donc 5p+1", tu peut aussi le rédiger en écrivant simplement que
Tu pouvait aussi un peu alléger le nombre de cas en écrivant qu'un entier non multiple de 5, non seulement on peut l'écrire avec , mais aussi sous la forme avec ce qui, au signe prés, ne fait que deux cas de figure (et comme on élève au carré, les signes disparaissent).

Pour l'exercice 139, il faut faire la même chose que pour le 136 mais en regardant le reste de la division par 8 du carré d'un entier quelconque (en considérant deux cas selon que l'entier est pair ou impair).
Ensuite, il faut regarder si en ajoutant 3 tels restes (de division par 8 d'un carré) est-ce qu'il est possible d'obtenir 7 (la réponse est "non").
Par contre, je vois pas vraiment l'intérêt de la question 1) qui risque d'embrouiller plus qu'autre chose.

Hello Ben, j'espère que tu va bien!
Merci pour ton aide je pourrai faire le 139 maintenant