Nombre complexe

[novak]

Bonsoir,

Quelqu'un pourrait il m'expliquer comment on calcul "sin n;)" et "cos n;)" en fonction de "sin ;)" et "cos ;)" ?

Merci

[cachender]

Je suis en terminal S aussi et c'est la formule de moivre selon laquelle :

( cos + isin ) = Cos n;) + i sin n;)

Tu attendais peut-être la démonstration ?

[axiome]

Bonsoir,
Il faut utiliser la formule de Moivre :

avec réel quelconque et n entier naturel.

[novak]

oui effectivement j'esperai la démonstration stp

[axiome]

Tu veux la démonstration de la formule de Moivre ?
Pas compliqué : un petit raisonnement par récurrence doit marcher...

[cachender]

Tu veux la démonstration de la formule de Moivre ?
Pas compliqué : un petit raisonnement par récurrence doit marcher...

Oui il faut utiliser le raisonnement de récurrence mais pas que cela c'est en réalité un peu plus compliqué le raisonnement par récurrence peut être appliqué que pour n >0

[axiome]

Oui il faut utiliser le raisonnement de récurrence mais pas que cela c'est en réalité un peu plus compliqué le raisonnement par récurrence peut être appliqué que pour n >0

Bah, de toute façon, la formule de Moivre n'est valable que pour n>0, je crois, non ?

[cachender]

Bah, de toute façon, la formule de Moivre n'est valable que pour n>0, je crois, non ?

Non je crois que n appartient a Z

[cachender]

En tout cas pour cette démonstration il faut que tu est vu le raisonnement par réccurence tu pars de z = cos + isin

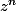
et = Cos n;) + i sin n;)

Tu calcule au rang 0 , au rang k et tu admet le rang k+1 et ça va tout seul

[novak]

hmm, je suis pas sur de savoir faire..

[axiome]

hmm, je suis pas sur de savoir faire..

C'est sûr que si tu n'as pas vu le raisonnement par récurrence, c'est un peu idiot de la part de ton prof de te donner un exo comme ça...

[cachender]

Calcule déjà au rang 0 :

= ...
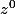
Cos 0;) + i sin 0;)= .... Donc tu conclu pour le rang 0 et tu admet que le rang k est vrai, cela te servira d'hypothèse

Tu n'as pas vu cela en cour ?