Bonjour tout le monde.
J'ai une question me posant un problème.
Voilà:
On sait que:
-Z=e^{i7Pi/ 12}
-cos (7Pi /12)= racine 2 /2
-sin (7Pi/12)=-racine 2/2
Ecrire sous forme algébrique le nombre complexe Z^2018
Il faut, je pense, utiliser ''2kPi'' mais je ne vois pas la démonstration
Et généralement, comment faire face à des questions du type Z^20...
Merci
Nombre complexe Z^2018
10 messages
- Page 1 sur 1
Re: Nombre complexe Z^2018
Bonjour Mimosa
Merci pour ta réponse.
Donc:
Z^12=(e^{i7Pi/12})^12=e^{i7Pi}=cos 7PI+i sin 7Pi=-1
Comme: 2018=2016+2=12*168+2
Alors:
Z^2018=(e^{i7Pi/12})^12*168+2=?
après cela je ne vois pas on ne peut pas faire (e^{i7Pi/12})^12*168+2=-1^170
Merci pour ta réponse.
Donc:
Z^12=(e^{i7Pi/12})^12=e^{i7Pi}=cos 7PI+i sin 7Pi=-1
Comme: 2018=2016+2=12*168+2
Alors:
Z^2018=(e^{i7Pi/12})^12*168+2=?
après cela je ne vois pas on ne peut pas faire (e^{i7Pi/12})^12*168+2=-1^170
Re: Nombre complexe Z^2018
Eh bien, ça donne
^{12})^{168}\times (-1)^2) .
.
En fait, j'espérais que tu verrais tout de suite que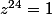 et que
et que 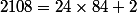
En fait, j'espérais que tu verrais tout de suite que
Re: Nombre complexe Z^2018
ah en effet,
Merci pour ton aide. la démonstration paraît très claire maintenant.
Merci beaucoup^^
Merci pour ton aide. la démonstration paraît très claire maintenant.
Merci beaucoup^^
Re: Nombre complexe Z^2018
Variante par le module 24 direct (je pense que c'est ce que tu voulais faire au départ)
Z=e^{i7Pi/ 12}
Z^2018 = (e^{i7Pi/ 12})^2018
Z^2018 =e^{i(7*2018)Pi/ 12}
2pi= 24pi/12
7*2018 modulo 24 = 14
Z^2018 =e^{i 14 Pi/ 12}
Z^2018 =e^{i 7 Pi/ 6}
Z^2018 =e^{i( Pi + Pi/ 6)}
facile à trouver sur le cercle trigo, ses sinus et cosinus sont opposés à ceux de e^ipi/6
Z=e^{i7Pi/ 12}
Z^2018 = (e^{i7Pi/ 12})^2018
Z^2018 =e^{i(7*2018)Pi/ 12}
2pi= 24pi/12
7*2018 modulo 24 = 14
Z^2018 =e^{i 14 Pi/ 12}
Z^2018 =e^{i 7 Pi/ 6}
Z^2018 =e^{i( Pi + Pi/ 6)}
facile à trouver sur le cercle trigo, ses sinus et cosinus sont opposés à ceux de e^ipi/6
Re: Nombre complexe Z^2018
Bonjour Pascal.
Merci pour ton aide
Désolé de te répéter, mais comment as tu trouvé: Z*2018 modulo 24 = 14
Merci pour ton aide
Désolé de te répéter, mais comment as tu trouvé: Z*2018 modulo 24 = 14
Re: Nombre complexe Z^2018
pas "z" mais "7*2018" sept fois 2018
sans utiliser la fonction "reste de la division entière" d la calculette
(2018*7)/24=588,xxxxx
2018*7 - 24*588 = 14
donc 2018*7 = 24*588 +14
version mimosa / spé math:
congruence modulo 24
2018*7 congru à (2018 modulo 24) * 7 = 2* 7 = 14
sans utiliser la fonction "reste de la division entière" d la calculette
(2018*7)/24=588,xxxxx
2018*7 - 24*588 = 14
donc 2018*7 = 24*588 +14
version mimosa / spé math:
congruence modulo 24
2018*7 congru à (2018 modulo 24) * 7 = 2* 7 = 14
Re: Nombre complexe Z^2018
7Pi/12 * 2018
ent((7*2018/12)/2) = 588
7Pi/12 * 2018 - 588 * 2Pi = Pi * (7 * 2018 - 588 * 2 * 12)/12 = 14/12 Pi = Pi + Pi/6
z^2018 = cos(Pi + Pi/6) + i.sin(Pi + Pi/6) = -cos(Pi/6) - i.sin(Pi/6)
z^2018 = -(V3)/2 - (1/2).i

ent((7*2018/12)/2) = 588
7Pi/12 * 2018 - 588 * 2Pi = Pi * (7 * 2018 - 588 * 2 * 12)/12 = 14/12 Pi = Pi + Pi/6
z^2018 = cos(Pi + Pi/6) + i.sin(Pi + Pi/6) = -cos(Pi/6) - i.sin(Pi/6)
z^2018 = -(V3)/2 - (1/2).i
Re: Nombre complexe Z^2018
Merci infiniment à tous pour votre aide.
En effet il faut utiliser la congruence .
merci encore^^
En effet il faut utiliser la congruence .
merci encore^^
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
