Bonjour j'ai un Devoir maison a rendre pour la rentré et moi aussi je coince un peu :
Tout d'abord je ne comprend pas la consigne d'un exercice:
Donner les valeur de X pour lesquelles les expressions suivantes sont définies :
F(x) = ;)(2x - 3) G(x) = ;)(x²+1) H(x) = 1/;)(x-4)
puis juste 3 factorisation :
B(x) = 5x² - 1
D(x) = 4x² + 4x;)(3) + 3
H(x) = 5x^3 - 2x² + 5x - 2
merci beaucoup d'avance! J'espère que vous allaient me débloqué =)
Niveaux 1 er S - Factorisation + 1 exercice non compri
12 messages
- Page 1 sur 1
ever-0 a écrit: Bonjour j'ai un Devoir maison a rendre pour la rentré et moi aussi je coince un peu :
Tout d'abord je ne comprend pas la consigne d'un exercice:
Donner les valeur de X pour lesquelles les expressions suivantes sont définies :
F(x) =(2x - 3) G(x) =
(x²+1) H(x) = 1/;)(x-4)
c'est tout simplement l'ensemble de définition de chaque fonction
ever-0 a écrit:puis juste 3 factorisation :
B(x) = 5x² - 1
D(x) = 4x² + 4x;)(3) + 3
H(x) = 5x^3 - 2x² + 5x - 2
merci beaucoup d'avance! J'espère que vous allaient me débloqué =)
il me semble que tu as appris des identités remarquables au collège non?
oscar a écrit:Bonsoir
B(x) =5x² -1 Formule a² -b²=
D(x) = 4x² -4xV3 +3 = formule a² -2ab +b²= .....
H(x) = 5x³ -2x² +5x -2 par groupements
(5x³ -5x) - (2x² +2) =...
C'est des identités remarquables du collège donc tu pourrais un peu le laisser chercher au lieu de lui donner à moitier les réponses. Il rentre surment en 1ère alors il doit être capable de faire ce genre de factorisation donc ne mache pas le travail stp
guigui51250 a écrit:C'est des identités remarquables du collège donc tu pourrais un peu le laisser chercher au lieu de lui donner à moitier les réponses. Il rentre surment en 1ère alors il doit être capable de faire ce genre de factorisation donc ne mache pas le travail stp
Je tien a dire a Guigui que tes remarque "il me semble que tu as appris des identités remarquables au collège non?" ou "c'est tout simplement l'ensemble de définition de chaque fonction" Ne m'ont absolument pas aidé, je sais qu'il ne faut pas "mâcher le travaille" mais la tu me laisse trop dans le flou (je suis rouillé après Deux moi ^^ )
Grâce à oscar j'ai pu comprendre que c'était les racine carré qui me bloqué =)
Merci a toi !
mais j'ai toujours pas compris le 1 er exercices =s
ever-0 a écrit:mais j'ai toujours pas compris le 1 er exercices =s
Pour le 2ème exercice pas de problème je laisse oscar te donner les réponse mais n'oublie pas qu'au moment où tu passeras le bac, oscar ne ce souviendra surment plus de toi et tu seras tout seul(e). Enfin je suis quand même là pour t'aider et je sors d'une 1èreS donc je sais de quoi je parle.
Concernant le 1er exercice, ce que l'on te demande est l'ensemble de définition de la fonction. Pour plus de précisions :
- une racine carrée est toujours positive donc ce qu'il y a "dessous" doit être positif tu comprends?
- le numérateur d'un quotient ne doit pas être égal à 0
guigui51250 a écrit:- une racine carrée est toujours positive donc ce qu'il y a "dessous" doit être positif tu comprends?
Heu Ahem Ahem
:doh: Ca n'a absolument RIEN A VOIR.
ce qui est vrai, c'est que comme un réel au carré est forcément positif, on ne peut prendre de racine carrée d'un réel négatif (cadre réel, j'insiste.)
ce qui est aussi vrai, c'est qu'une racine carrée est positive par convention.
un petit cumul cher guigui ;
L.A. a écrit:Heu Ahem Ahem
:doh: Ca n'a absolument RIEN A VOIR.
ce qui est vrai, c'est que comme un réel au carré est forcément positif, on ne peut prendre de racine carrée d'un réel négatif (cadre réel, j'insiste.)
ce qui est aussi vrai, c'est qu'une racine carrée est positive par convention.
un petit cumul cher guigui ;
bah ce que je voulais dire c'est que ce qu'il y a sous la racine ne peut pas être négatif, tu es bien dacord avec moi non?
Salut,
Le «donc» est au moins abusif.
Pour être plus précis :
-- les nombres négatifs n'ont pas de racine carrée réelle
-- la fonction associe à chaque réel positif
associe à chaque réel positif  le réel positif
le réel positif  tel que
tel que 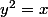 .
.
Il est à remarquer que si on avait choisi le réel négatif tel que
tel que 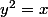 ça ne changerait rien au domaine de d&finition de la fonction.
ça ne changerait rien au domaine de d&finition de la fonction.
guigui51250 a écrit:[...]
- une racine carrée est toujours positive donc ce qu'il y a "dessous" doit être positif tu comprends?
[...]
Le «donc» est au moins abusif.
Pour être plus précis :
-- les nombres négatifs n'ont pas de racine carrée réelle
-- la fonction
Il est à remarquer que si on avait choisi le réel négatif
nuage a écrit:Salut,
Le «donc» est au moins abusif.
Pour être plus précis :
-- les nombres négatifs n'ont pas de racine carrée réelle
-- la fonctionassocie à chaque réel positif
le réel positif
tel que
.
Il est à remarquer que si on avait choisi le réel négatiftel que
ça ne changerait rien au domaine de d&finition de la fonction.
oui mais comme tu l'as dit, "les nombres négatifs n'ont pas de racine carrée réelle" c'est ça que je voulais dire. Je me suis peut-être mal exprimé et désolé si ça vous à embrouiller mais je voulais dire que les nombres négatifs n'ont pas de racine carrée réelle c'est tout.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
