Négation d'une propositition quantifiée

par **alexis6** » 28 Mar 2015, 12:28

Bonjour,

En général il est facile de faire la négation de propositions quantifiées, il suffit de remplacer les " il existe " en " pour tout ", et inversement. Quelquefois c'est un peu plus complexe. Je m'explique à l'aide d'un exemple:

Si on doit faire la contraposée de:

,

ce sera:

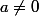
Pour passer de ça

à ça

, on a changé le " pour tout " en " il existe " , mais on a seulement changé un des deux comparants. Comment cela se fait?

Et en général, quelle est la différence entre une proposition avec des " tels que ", par rapport à une proposition où l'on met des virgules?

par **capitaine nuggets** » 28 Mar 2015, 12:35

Salut !

La négation de "

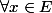
tel que

vérifie une propriété

" est "

tel que

ne vérifie pas la propriété

".

:+++:

par **alexis6** » 28 Mar 2015, 12:43

capitaine nuggets a écrit:Salut !

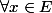
La négation de " tel que vérifie une propriété " est " tel que ne vérifie pas la propriété ".

:+++:

Ok mais comment fiare dans ce cas pour une propriété P de faire en sorte que elle ne soit pas vérifiée. Si on a par exemple:

la propriété a>k,b>3,c=7,c>k,b<c.

Comment faire quand les différentes variables sont liées?

par **capitaine nuggets** » 28 Mar 2015, 12:59

[quote="alexis6"]Ok mais comment fiare dans ce cas pour une propriété P de faire en sorte que elle ne soit pas vérifiée. Si on a par exemple:

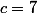
la propriété a>k,b>3,c=7,c>k,bk[/TEX] ET

ET

" alors tu as "

ET

".
Donc la négation est "

OU

"

(la néagation de "

" est la négation de "

ET

")

la négation de x vérifie "P" ET x vérifie "Q" est x ne vérifie pas "P" OU x ne vérifie pas "Q" (x peut éventuellement ne pas vérifier les deux propriétés).

:++:

par **alexis6** » 28 Mar 2015, 14:18

Ok merci beaucoup. Un truc vraiment simple, je n'avais pas compris que la virgule, c'était le connecteur "et"... Et le " tel que ", c'est aussi le "et" du coup? Quelle différence?

Sinon, si j'ai bien compris, la négation de:

peut aussi bien être ça

que ça

non? é

Je ne sais pas trop pour ça, parce que pour moi, il n'y a qu'une seule propriété accompagnée d'une quantification, donc logiquement, on ne peut pas nier la quantification et la considérer comme une propriété non?

par **nodjim** » 28 Mar 2015, 15:09

Je suis un peu d'avis d'Alexis. "Quel que soit" est le début d'une proposition, alors que "il existe" est le début d'une affirmation. De plus, un x dans un ensemble E qui satisfait à une propriété P ne donne pas l'assurance qu'il existe un autre x de E qui ne satisfait pas cette propriété.

par **capitaine nuggets** » 28 Mar 2015, 15:16

alexis6 a écrit:Ok merci beaucoup. Un truc vraiment simple, je n'avais pas compris que la virgule, c'était le connecteur "et"... Et le " tel que ", c'est aussi le "et" du coup? Quelle différence?

Sinon, si j'ai bien compris, la négation de: peut aussi bien être ça que ça non? é

Je ne sais pas trop pour ça, parce que pour moi, il n'y a qu'une seule propriété accompagnée d'une quantification, donc logiquement, on ne peut pas nier la quantification et la considérer comme une propriété non?

J'ai un peu de mal à comprendre ce que tu veux dire mais c'est vrai que la virgule ne représente pas un "ET" normalement, sauf que des fois on l'assimile à ça...

par **alexis6** » 28 Mar 2015, 16:25

En fait, je n'ai pas les idées claires quand il s'agit de nier une proposition, spécialement quand c'est une proposition quantifiée. J'ai plusieurs problèmes.

1er problème:

Dans mon chapitre de logique, on écrit qu'il y a 5 connecteurs: union, intersection, implication, équivalence, négation. Je sais faire la négation de ces connecteurs. Or dès que l'on passe à des propositions quantifiées, on a également comme connecteur la virgule, et le " tel que ". Ceux-là je ne sais pas les nier, je ne sais pas ce qu'ils représentent.

2ème problème

J'ai du mal à savoir si dans une proposition du type : " il existe x appartenant à A tel que P(x) " ou " pour tout x appartenant à A tel que P(x) " ce qu'il faut nier. On fait la négation de P(x)? La négation de " x appartenant à A "? La négation de "x appartenant à A ET P(X)"? La négation de "x appartenant à A OU P(x)"?

Bref c'est encore flou pour moi...

par **nodjim** » 29 Mar 2015, 10:25

Définition: Soit P une propriété sur l'ensemble E. Une propriété Q sur E est une "négation" de P si et seulement si, pour tout x :

- Q(x) est F si P(x) est V

- Q(x) est V si P(x) est F

Négation d'une propositition quantifiée

Négation d'une propositition quantifiée

Qui est en ligne