Need help
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

 par pierrelouisbourgeois » 25 Fév 2020, 19:43
par pierrelouisbourgeois » 25 Fév 2020, 19:43
Bonsoir,
Je cherche à trouver
)
sachant que
 = e^{kx})
avec x qui appartient à R et k à N
(je cherche à démontrer que quand on a
= e^{kx})
alors
= ke^{kx})
)
Merci et bonne soirée
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 25 Fév 2020, 20:21
par GaBuZoMeu » 25 Fév 2020, 20:21
C'est un cas très simple de dérivée de fonction composée : la fonction

suivie par la fonction
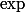
.

 par pierrelouisbourgeois » 25 Fév 2020, 21:25
par pierrelouisbourgeois » 25 Fév 2020, 21:25
Merci pour votre réponse mais en fait j'ai l'impression de tourner en rond ;
On a :

avec


ainsi,

et
 = g'(e^{kx})\times e^{kx})
Je ne vois pas comment avancer...
-
mathelot
 par mathelot » 25 Fév 2020, 21:43
par mathelot » 25 Fév 2020, 21:43
pierrelouisbourgeois a écrit:Je cherche à trouver
)
sachant que
 = e^{kx})
avec x qui appartient à R et k à N
(je cherche à démontrer que quand on a
= e^{kx})
alors
= ke^{kx})
)
Merci et bonne soirée
ta notation est hasardeuse car g'(e^x) signifie la dérivée de g évaluée au point e^x et non pas ce que tu cherches , à savoir la dérivée de
)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
sachant que
avec x qui appartient à R et k à N
alors
)