Bonjour!
Je dois faire un exercice sur le produit scalaire ( enfin je suis presque sur que c'est à propos de ça ), mais malgrè y avoir beaucoup de temps, je ne trouve pas la solution. L'énoncé est le suivant :
Le triangle AOB est rectangle en O. I est le milieu de [AB] et H est le projeté orthogonale de O sur [AB]. Le point H se projette orthogonalement en J sur (OA) et en K sur (OB). Faire la figure et montrer que les droites (OI) et (JK) sont perpendiculaires.
Je suis vraiment bloqué, et si vous pouviez m'aider ce serait vraiment génial...
Merci et bonne journée.
Montrer une orthogonalité, produit scalaire?
10 messages
- Page 1 sur 1
Méthode 2 : La mienne
Sans aucun repère.
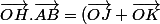.(\frac{1}{2}\vec{OA}+\frac{1}{2}\vec{OB}))
En réduisant ceci, puis en factorisant par 1/2 :
)
Or, on sait que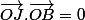 et que
et que 
donc l'expression s'écrit également: ( l'astuce est d'ajouter ceci à l'égalité ... ou de le retrancher !! )
)
et par factorisation, on retrouve
)
encore une factorisation:
)
on en déduit donc que
si tu as des problèmes sur les factorisations que tu trouve pas super triviales pour toi, dis le moi ...
Sans aucun repère.
En réduisant ceci, puis en factorisant par 1/2 :
Or, on sait que
donc l'expression s'écrit également: ( l'astuce est d'ajouter ceci à l'égalité ... ou de le retrancher !! )
et par factorisation, on retrouve
encore une factorisation:
on en déduit donc que
si tu as des problèmes sur les factorisations que tu trouve pas super triviales pour toi, dis le moi ...
en fait c'est super simple avec la RDC:
on est d'accord que ( tout en vecteur) :
OI.JK=(OB+BI).(JO+OK)=OB.OK+BI.JO+BI.OK
or par projection orthogonale : BI.OK=BI.HK et par égalité, BI.JO=BI.HK donc l'égalité se réécrit :
OI.JK=OB.OK+2BI.HK=OB.OK+BA.HK
or OB.OK=AB.OK=-BA.OK
on réécrit :
OI.JK=BA.HK-BA.OK=BA.(HK-OK)=BA.HO=0 CQFD,
en espérant avoir été clair :)
on est d'accord que ( tout en vecteur) :
OI.JK=(OB+BI).(JO+OK)=OB.OK+BI.JO+BI.OK
or par projection orthogonale : BI.OK=BI.HK et par égalité, BI.JO=BI.HK donc l'égalité se réécrit :
OI.JK=OB.OK+2BI.HK=OB.OK+BA.HK
or OB.OK=AB.OK=-BA.OK
on réécrit :
OI.JK=BA.HK-BA.OK=BA.(HK-OK)=BA.HO=0 CQFD,
en espérant avoir été clair :)
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 90 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
