La monotonie de f
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
SamiaEl
- Membre Naturel
- Messages: 26
- Enregistré le: 20 Nov 2018, 20:45
-
 par SamiaEl » 21 Nov 2018, 14:40
par SamiaEl » 21 Nov 2018, 14:40
Salut , est ce que vous pouvez m'aider ??
Soit f le fonction définie par f(x)=x/(√(x²+1))
1/Déterminer le Df puis montrer que f est impaire :Df=R
On a f(-x)=-x/(√(x²+1)) = -f(x)
Donc f est impaire
2/Montrer que -1<f(x)<1 pour quelque soit x de R :On a x²+1>x²
Donc √(x²+1)>lxl
Alors - √(x²+1)< x<√(x²+1)
D’ où -1<x/(√(x²+1))<1
3/Montrer que ( f(x))²=1- 1/(1+x²) on a (f(x))²-1/(x²+1) = 0
donc f(x))²=1- 1/(1+x²)
4/Etudier la monotonie de f sur Df J'ai essayer d'utiliser le taux de variation mais j'ai pas trouver la solution
Est ce que les autres sont justes??
Merci d'avance


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 21 Nov 2018, 15:01
par chan79 » 21 Nov 2018, 15:01
salut
pour la 3
(f(x))²=x²/(x²+1)
montre que c'est égal à 1-1/(x²+1)
Si tu as une fonction f positive sur un intervalle, et si son carré est une fonction croissante, que peux tu dire de f ?
-
SamiaEl
- Membre Naturel
- Messages: 26
- Enregistré le: 20 Nov 2018, 20:45
-
 par SamiaEl » 21 Nov 2018, 15:10
par SamiaEl » 21 Nov 2018, 15:10
J'ai montrer que leur différence égale 0 donc ils sont égaux est ce que c'est faux ??
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 21 Nov 2018, 15:15
par Carpate » 21 Nov 2018, 15:15
Monotonie de f (avec les taux de variation)Il suffit de l'établir sur R+ puis de la déduire sur R par suite de l'imparité de f.
Soient

, montre que
-f(a)}{b-a}=\frac{b\sqrt{a^2+1}-a\sqrt{b^2+1}}{\sqrt{(a^2+1)(b^2+1)}}=\frac{b^2-a^2}{(b-a)(b\sqrt{a^2+1}+a\sqrt{b^2+1})\sqrt{(a^2+1)(b^2+1)}}=\frac{b+a}{(b\sqrt{a^2+1}+a\sqrt{b^2+1})\sqrt{(a^2+1)(b^2+1)}})
Modifié en dernier par
Carpate le 21 Nov 2018, 16:17, modifié 2 fois.
-
SamiaEl
- Membre Naturel
- Messages: 26
- Enregistré le: 20 Nov 2018, 20:45
-
 par SamiaEl » 21 Nov 2018, 15:24
par SamiaEl » 21 Nov 2018, 15:24
chan79 a écrit: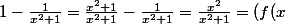)^2)
la croissance de f peut se déduire de celle de f² sur
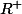
Merci mais est ce que vous pouvez m'indiquer comment??
-
SamiaEl
- Membre Naturel
- Messages: 26
- Enregistré le: 20 Nov 2018, 20:45
-
 par SamiaEl » 21 Nov 2018, 15:25
par SamiaEl » 21 Nov 2018, 15:25
chan79 a écrit:salut
pour la 3
(f(x))²=x²/(x²+1)
montre que c'est égal à 1-1/(x²+1)
Si tu as une fonction f positive sur un intervalle, et si son carré est une fonction croissante, que peux tu dire de f ?
Est ce qu'on peut dire que f est croissante aussi, si son carrée est croissant ??

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 21 Nov 2018, 16:04
par chan79 » 21 Nov 2018, 16:04
Suppose que f soit positive sur un intervalle est que son carré soit une fonction croissante
si x<y alors (f(x))²<(f(y))² donc |f(x)| <|f(y)| et donc f(x) < f(y) si f est postitive
-
SamiaEl
- Membre Naturel
- Messages: 26
- Enregistré le: 20 Nov 2018, 20:45
-
 par SamiaEl » 21 Nov 2018, 19:46
par SamiaEl » 21 Nov 2018, 19:46
Bon je pense que j'ai trouvé la solution merci de me corrigée
on a (f(x))²-(f(y))²=(x²-y²)/((x²+1)(y²+1))
(f(x)-f(y)) (f(x)+f(y))=(x²-y²)/((x²+1)(y²+1))
Soit x,y appartient à [0,+infini[
Donc x²+1>0 et y²+1>0 et f(x)+f(y)>0
Si x<y donc (x²-y²)/((x²+1)(y²+1))
donc f(x)-f(y)<0
f(x)<f(y)
Donc f croissante sur [0,+infini[
puisqu'il est pair don il est croissante sur ]-infini,0]
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 21 Nov 2018, 20:08
par Carpate » 21 Nov 2018, 20:08
j'ai trouvé la solution merci de me corrigée
horreur : j'ai trouvé la solution merci de me corriger
Si x<y donc (x²-y²)/((x²+1)(y²+1))
Déduction bizarre !
Donc f croissante sur [0,+infini[
puisqu'il est pair donc il est croissante sur ]-infini,0]
Manque de chance f n'est pas paire mais impaire
Si f était paire f serait décroissante sur
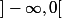
-
SamiaEl
- Membre Naturel
- Messages: 26
- Enregistré le: 20 Nov 2018, 20:45
-
 par SamiaEl » 21 Nov 2018, 20:23
par SamiaEl » 21 Nov 2018, 20:23
Carpate a écrit: j'ai trouvé la solution merci de me corrigée
horreur : j'ai trouvé la solution merci de me corriger
Si x<y donc (x²-y²)/((x²+1)(y²+1))
Déduction bizarre !
Donc f croissante sur [0,+infini[
puisqu'il est pair donc il est croissante sur ]-infini,0]
Manque de chance f n'est pas paire mais impaire
Si f était paire f serait décroissante sur
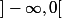
Oui c'est impaire
pour la déduction c'est
Si x<y donc (x²-y²)/((x²+1)(y²+1))<0
-
SamiaEl
- Membre Naturel
- Messages: 26
- Enregistré le: 20 Nov 2018, 20:45
-
 par SamiaEl » 21 Nov 2018, 20:24
par SamiaEl » 21 Nov 2018, 20:24
Pardon pour c'est petit faute je suis nouvelle et je trouve des difficultés merci
est ce que ma méthode est fausse?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 21 Nov 2018, 20:32
par Carpate » 21 Nov 2018, 20:32
Sur

, f(x) est positive et donc la démonstration de chan79 s'applique :
Suppose que f soit positive sur un intervalle et que son carré soit une fonction croissante
si x<y alors (f(x))²<(f(y))² donc |f(x)| <|f(y)| et donc f(x) < f(y) si f est postitive
Elle ne te convient pas ?
Elle est moins calculatoire que si l'on utilise les taux de variation.
Modifié en dernier par
Carpate le 21 Nov 2018, 20:39, modifié 2 fois.
-
SamiaEl
- Membre Naturel
- Messages: 26
- Enregistré le: 20 Nov 2018, 20:45
-
 par SamiaEl » 21 Nov 2018, 20:35
par SamiaEl » 21 Nov 2018, 20:35
Oui j'ai essayé avec taux de variation mais je suis bloqué dans le calcule
Est - ce - que j'ai commis une faute dans la démonstration
Merci

-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 21 Nov 2018, 20:49
par Carpate » 21 Nov 2018, 20:49
(f(x))²-(f(y))²=(x²-y²)/((x²+1)(y²+1))
Erreur :
-f^2(y)=\frac{x^2}{1+x^2}-\frac{y^2}{1+y^2}=\frac{x^2(y^2+1)-y^2(x^2+1)}{(1+x^2)(1+y^2)}<br />=\frac{x^2-y^2}{(1+x^2)(1+y^2)})
-
SamiaEl
- Membre Naturel
- Messages: 26
- Enregistré le: 20 Nov 2018, 20:45
-
 par SamiaEl » 21 Nov 2018, 20:53
par SamiaEl » 21 Nov 2018, 20:53
Carpate a écrit: (f(x))²-(f(y))²=(x²-y²)/((x²+1)(y²+1))
Erreur :
-f^2(y)=\frac{x^2}{1+x^2}-\frac{y^2}{1+y^2}=\frac{x^2(y^2+1)-y^2(x^2+1)}{(1+x^2)(1+y^2)}<br />=\frac{x^2-y^2}{(1+x^2)(1+y^2)})
C'est ce que j'ai fait
(x²-y²)
/((x²+1)(y²+1))
-
SamiaEl
- Membre Naturel
- Messages: 26
- Enregistré le: 20 Nov 2018, 20:45
-
 par SamiaEl » 21 Nov 2018, 20:54
par SamiaEl » 21 Nov 2018, 20:54
SamiaEl a écrit: Carpate a écrit: (f(x))²-(f(y))²=(x²-y²)/((x²+1)(y²+1))
Erreur :
-f^2(y)=\frac{x^2}{1+x^2}-\frac{y^2}{1+y^2}=\frac{x^2(y^2+1)-y^2(x^2+1)}{(1+x^2)(1+y^2)}<br />=\frac{x^2-y^2}{(1+x^2)(1+y^2)})
C'est ce que j'ai fait
(x²-y²)
/((x²+1)(y²+1))
(x²-y²)
/ ((x²+1)(y²+1)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 21 Nov 2018, 20:57
par Carpate » 21 Nov 2018, 20:57
Ah pardon, je n'avais pas compris ton raccourci mais reconnais que ça mérite un petit calcul intermédiaire ...
-
SamiaEl
- Membre Naturel
- Messages: 26
- Enregistré le: 20 Nov 2018, 20:45
-
 par SamiaEl » 21 Nov 2018, 20:59
par SamiaEl » 21 Nov 2018, 20:59
D'accord merci^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
