Méthode de résolution?

[pierrelouisbourgeois]

Bonjour,

J'aimerai savoir comment déterminer les triplets entiers p,q,r solutions de :



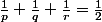
sachant que p<=q<=r

Est-ce qu'il y a une méthode ?

Bonne journée et merci.

[GaBuZoMeu]

Pour commencer, on sait que . Tu vois pourquoi ?

[pierrelouisbourgeois]

Non

[LB2]

Si p = 1 ou p = 2, a-t-on des solutions ?
Même question pour p = 7 ou plus

[GaBuZoMeu]

Ne pas oublier la condition

[pierrelouisbourgeois]

Pas de solution pour p = 1 car la somme serait > à 1/2 (au minimum = 3)
Pas de solution pour p = 2 car la somme serait > à 1/2 (au minimum = 3/2)
Pour p = 3, il semble que ça serait possible
pareil pour p=4 p=5 et p=6

Et au delà de p=6, pour p= 7, on aurait dans le meilleur cas
1/7 + 1/7+1/7 = 3/7 < 1/2 et plus p sera grand, plus la somme diminuera donc pas de solution

[GaBuZoMeu]

Ben voila, tu as un début de méthode, yapuka continuer.
Je trouve 10 triplets solutions, mais je me suis peut-être trompé.

[Black Jack]

11 triplets solutions :

0, 0 ,0
3, 7,42
3, 8, 24
3, 9, 18
3, 10, 15
3, 12, 12
4, 5, 20
4, 6, 12
4, 8, 8
5, 5, 10
6, 6, 6

[GaBuZoMeu]

1°) Pourquoi donner la solution ?
2°) Pourquoi donner une solution fausse (0,0,0)

[pierrelouisbourgeois]

J'en trouve 10 aussi... Mais GaBuZoMeu, est-ce qu'il y a une méthode pour ce genre d'équations ? Ou bien est-ce qu'il faut toujours chercher comme ça ? (il n'y a pas une affaire de majorant/minorant?)

[GaBuZoMeu]

Il me semble bien t'avoir indiqué une méthode qui consiste à minorer et majorer : s'il y a une solution (p, q, r) alors p est entre 3 et 6. Puis on continue : s'il y a une solution (3, q, r), alors q est entre 7 et 12 ; s'il y a une solution (4, q, r), alors q est entre 5 et 8 etc..

[pierrelouisbourgeois]

D'accord merci pour l'aide

[LB2]

L'argument d'encadrement permet de se ramener à un ensemble fini de candidats (car on cherche uniquement les entiers). La réciproque est alors facile.

[Black Jack]

2°) Pourquoi donner une solution fausse (0,0,0)

Parce que j'ai inclus accidentellement par distraction un triplet (0;0;0) issu d'un autre topic.
Voila ce qui peut arriver en faisant plusieurs choses simultanément.