Méthode pour multiples équations
21 messages
- Page 1 sur 2 - 1, 2
méthode pour multiples équations
Bonsoir tous le monde, première chose je vous remercie énormément pour votre aide pour le système d'axe orthogonal grâce a vous jai compris tous de suite comment ça fonctionné.
Mais aujourdhui jaurais besoin de votre aide pour les équations a 3 et voir plus dinconnues pour se qui est des 3 jutilise la méthode cramer mais je voudrais maitriser une autre méthode pour réaliser des 4, 5, voir plus dinconnue alors si quelquun saurait quel méthode utiliser pour résoudre ces équations (3, 4,5, . Inconnues) et si vous pouviez en faire une avec une petite explication se serais super sympa.
Merci davance et je vous souhaite a tous une très bonne soirée et une longue vie au forum.
Mais aujourdhui jaurais besoin de votre aide pour les équations a 3 et voir plus dinconnues pour se qui est des 3 jutilise la méthode cramer mais je voudrais maitriser une autre méthode pour réaliser des 4, 5, voir plus dinconnue alors si quelquun saurait quel méthode utiliser pour résoudre ces équations (3, 4,5, . Inconnues) et si vous pouviez en faire une avec une petite explication se serais super sympa.
Merci davance et je vous souhaite a tous une très bonne soirée et une longue vie au forum.
Je vois ce que tu veux dire. Nous allons donc voir tranquillement les différentes notions.
Au lycée et au collège, en France, on voit principalement une sorte de système : les systèmes linéaires.
Les systèmes linéaires sont de la forme :

Ce système possède n équations et p inconnues.
On apprend classiquement à résoudre des systèmes qui ont autant d'équations que d'inconnues, ce sont les fameux systèmes "carrés".
Chaque solution du système (ici les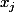 où j vaut 1, 2, 3, ...) est appelé un p-uplet.
où j vaut 1, 2, 3, ...) est appelé un p-uplet.
On dit que deux systèmes d'équations linéaires sont de même taille lorsque leur ensemble de solutions est le même.
Pour résoudre un système, notre premier outil est l'utilisation des opérations élémentaires.
Exemple : soit (S) le système tel que :

Ce système a 3 inconnues (x, y et z) et trois équations.
Si j'additionne la première et la troisième ligne ensemble j'obtiens le système :

Si je regarde les deux dernières lignes je vois y-z=1 et -y+z=0.
Existe-t-il deux réels qui respectent ces conditions ? Non, donc le système n'a pas de solution.
La méthode du pivot de Gauss consiste à effectuer des opérations à partir d'un pivot. On appelle aussi ce principe méthode par substitution ou méthode par combinaison (selon les cas).
Exemple : Soit (T) le système tel que :
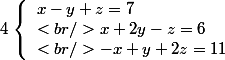
Ici je marche par combinaison entre les deux premières lignes, le but étant d'isoler une inconnue.
Essaye de le faire !
Au lycée et au collège, en France, on voit principalement une sorte de système : les systèmes linéaires.
Les systèmes linéaires sont de la forme :

Ce système possède n équations et p inconnues.
On apprend classiquement à résoudre des systèmes qui ont autant d'équations que d'inconnues, ce sont les fameux systèmes "carrés".
Chaque solution du système (ici les
On dit que deux systèmes d'équations linéaires sont de même taille lorsque leur ensemble de solutions est le même.
Pour résoudre un système, notre premier outil est l'utilisation des opérations élémentaires.
Exemple : soit (S) le système tel que :
Ce système a 3 inconnues (x, y et z) et trois équations.
Si j'additionne la première et la troisième ligne ensemble j'obtiens le système :
Si je regarde les deux dernières lignes je vois y-z=1 et -y+z=0.
Existe-t-il deux réels qui respectent ces conditions ? Non, donc le système n'a pas de solution.
La méthode du pivot de Gauss consiste à effectuer des opérations à partir d'un pivot. On appelle aussi ce principe méthode par substitution ou méthode par combinaison (selon les cas).
Exemple : Soit (T) le système tel que :
Ici je marche par combinaison entre les deux premières lignes, le but étant d'isoler une inconnue.
Essaye de le faire !
Pour revenir sur la méthode matricielle, c'est complètement barbant d'inversé une matrice ( faut déjà calculer le det. afin de voir si elle est inversible et on galère déjà) . La méthode matricielle n'est utilisée que par les calculettes, à la main c'est plus long qu'avec le pivot de gauss. Enfin, c'est ce que je pense, je peut me tromper^^
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 107 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
