Méthode de Hörner
13 messages
- Page 1 sur 1
Méthode de Hörner
Bonjour . comment peut on factoriser le polynôme P défini sur R par P(x)= (a-1)x^3 + a (1-a^3)x^2+ a(a^3-1)x + (1-a) a^6 en utilisant la méthode de Horner ? (a est un réel différent de 1). j'ai vu un tableau avec une colonne avec a -1 et 0 en dessous mais je comprends pas trop... merci
Bah, je ne sais pas, je te demande.
Si a et a² sont racines de P alors ils vérifient nécessairement :
P(a)=0 et P(a²)=0.
Mais à mon avis cela m'étonnerai.
Essaye de calculer P(x) pour x= -3, -2, -1, 0, 1, 2 et 3.
Tiens moi au courant si pour une de ces valeurs P(x)=0.
Je ne connais qu'une méthode ou une racine est connue pour le degré 3, sinon, je pense pas pouvoir t'aider :triste:
Si a et a² sont racines de P alors ils vérifient nécessairement :
P(a)=0 et P(a²)=0.
Mais à mon avis cela m'étonnerai.
Essaye de calculer P(x) pour x= -3, -2, -1, 0, 1, 2 et 3.
Tiens moi au courant si pour une de ces valeurs P(x)=0.
Je ne connais qu'une méthode ou une racine est connue pour le degré 3, sinon, je pense pas pouvoir t'aider :triste:
Salut,
Ton polynôme est donc :
= (a-1)x^3 + a (1-a^3)x^2+ a^3(a^3-1)x + (1-a) a^6)
Effectivement et
et  sont des racines de P.
sont des racines de P.
Comme est racine de P, c'est que
est racine de P, c'est que =(x-a^2)\times(...)) et, comme P est de degrés 3, le
et, comme P est de degrés 3, le ) et de degrés 2 et on doit avoir :
et de degrés 2 et on doit avoir :
x^3 + a (1-a^3)x^2+ a^3(a^3-1)x + (1-a) a^6=(x-a^2)(?x^2+?x+?))
Si on développe le terme de droite, le terme en s'obtient en faisant
s'obtient en faisant  .
.
Comme ce terme doit valoirx^3) , c'est que
, c'est que 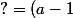) :
:
x^3 + a (1-a^3)x^2+ a^3(a^3-1)x + (1-a) a^6=(x-a^2)\big((a-1)x^2+?x+?\big))
Si on développe le terme de droite, le terme en s'obtient en faisant
s'obtient en faisant x^2) .
.
Comme ce terme doit valoirx^2) , c'est que
, c'est que 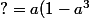+a^2(a-1)=a(1-a^3+a^2-a)=a(1-a)(1+a^2)) :
:
x^3 + a (1-a^3)x^2+ a^3(a^3-1)x + (1-a) a^6=(x-a^2)\big((a-1)x^2+a(1-a)(1+a^2)x+?\big))
Si on développe le terme de droite, le terme en s'obtient en faisant
s'obtient en faisant (1+a^2)) .
.
Comme ce terme doit valoirx) , c'est que
, c'est que 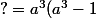+a^3(1-a)(1+a^2)=a^3(a^3-1+1+a^2-a-a^3)=a^4(a-1)) :
:
x^3 + a (1-a^3)x^2+ a^3(a^3-1)x + (1-a) a^6=(x-a^2)\big((a-1)x^2+a(1-a)(1+a^2)x+a^4(a-1)\big))
Enfin, pour vérifier que l'on ne s'est pas trompé, on regarde le terme constant obtenu en développant :=a^6(1-a)) O.K.
O.K.
La "méthode de Horner", c'est ça présenté dans un tableau.
Ton polynôme est donc :
Effectivement
Comme
Si on développe le terme de droite, le terme en
Comme ce terme doit valoir
Si on développe le terme de droite, le terme en
Comme ce terme doit valoir
Si on développe le terme de droite, le terme en
Comme ce terme doit valoir
Enfin, pour vérifier que l'on ne s'est pas trompé, on regarde le terme constant obtenu en développant :
La "méthode de Horner", c'est ça présenté dans un tableau.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
merci pour ta réponse très détaillée. j'ai trouvé un tableau sur internet qui calcule avec cette méthode P(a) et P(a²).
Voici le tableau :
[url="http://www.hebergementimages.com/image-d02279cb130a4ebf4cf39d7674ddca14_Sans-titre.PNG.html"] [/url]
[/url]
Si je comprends bien, en tête de colonne, il y a les coeff du polynôme, c'est ça ?
Et comment fait on ensuite pour arriver à ce tableau ?
merci
Voici le tableau :
[url="http://www.hebergementimages.com/image-d02279cb130a4ebf4cf39d7674ddca14_Sans-titre.PNG.html"]
 [/url]
[/url]Si je comprends bien, en tête de colonne, il y a les coeff du polynôme, c'est ça ?
Et comment fait on ensuite pour arriver à ce tableau ?
merci
Bon, il m'a fallut 2 plombes pour comprendre à quoi correspond ton tableau...
Les trois premières lignes correspondent à la division de P(x) par (x-a) :
Dans la première ligne tu met les coeffs de P puis tu procède colonne par collone (uniquement pour les lignes 2 et 3) :
Première colonne : en C1L2 (colonne1, ligne 2) tu met mécaniquement un 0 (à partir de la colonne 2, on mettra le reste du "coup d'avant" mais là, il y a pas de "coup d'avant) puis dans C1L3 tu met la somme C1L1+C1L2 donc ici (a-1)+0=a-1
Deuxième colonne : en C2L2 tu met 'a' (car on divise par x-a) fois le contenu de la case C1L3 c'est à dire a.(a-1)=a²-a puis en C2L3 tu met la somme C2L1+C2L2, c'est à dire a(1-a^3)+(a²-a)=a²-a^4.
Troisième colonne : en C3L2 tu met 'a' fois le contenu de la case C2L3 c'est à dire a.(a^2-a^4)=a^3-a^5 puis en C3L3 tu met la somme C3L1+C3L2, c'est à dire a^3(a^3-1)+(a^3-a^5)=a^6-a^5.
Quatrième colonne : en C4L2 tu met 'a' fois le contenu de la case C3L3 c'est à dire a.(a^6-a^5)=a^7-a^6 puis en C4L3 tu met la somme C4L1+C4L2, c'est à dire (1-a)a^6+(a^7-a^6)=0.
Le fait que tu trouve 0 à la fin montre que ton polynôme est bien divisible par (x-a).
Essaye de faire la division de P par (x-a) en présentant comme dans mon précedent post et tu constatera que ce sont exactement les mêmes calculs que ceux que l'on vient de faire ici. Seule la présentation est différente (la présentation sous forme de tableau permet d'économiser de l'encre mais j'aime pas bien cette méthode du fait que celui qui l'a jamais vu, et bien y capte que dalle à ce qu'on fait comme calculs et pourquoi ça marche)
Enfin les 3 dernières lignes du tableau correspondent à la division de (a-1)x²+(a^2-a^4)x+(a^6-a^5) [qui est le résultat obtenu lors de la première division] par (x-a^2).
Les trois premières lignes correspondent à la division de P(x) par (x-a) :
Dans la première ligne tu met les coeffs de P puis tu procède colonne par collone (uniquement pour les lignes 2 et 3) :
Première colonne : en C1L2 (colonne1, ligne 2) tu met mécaniquement un 0 (à partir de la colonne 2, on mettra le reste du "coup d'avant" mais là, il y a pas de "coup d'avant) puis dans C1L3 tu met la somme C1L1+C1L2 donc ici (a-1)+0=a-1
Deuxième colonne : en C2L2 tu met 'a' (car on divise par x-a) fois le contenu de la case C1L3 c'est à dire a.(a-1)=a²-a puis en C2L3 tu met la somme C2L1+C2L2, c'est à dire a(1-a^3)+(a²-a)=a²-a^4.
Troisième colonne : en C3L2 tu met 'a' fois le contenu de la case C2L3 c'est à dire a.(a^2-a^4)=a^3-a^5 puis en C3L3 tu met la somme C3L1+C3L2, c'est à dire a^3(a^3-1)+(a^3-a^5)=a^6-a^5.
Quatrième colonne : en C4L2 tu met 'a' fois le contenu de la case C3L3 c'est à dire a.(a^6-a^5)=a^7-a^6 puis en C4L3 tu met la somme C4L1+C4L2, c'est à dire (1-a)a^6+(a^7-a^6)=0.
Le fait que tu trouve 0 à la fin montre que ton polynôme est bien divisible par (x-a).
Essaye de faire la division de P par (x-a) en présentant comme dans mon précedent post et tu constatera que ce sont exactement les mêmes calculs que ceux que l'on vient de faire ici. Seule la présentation est différente (la présentation sous forme de tableau permet d'économiser de l'encre mais j'aime pas bien cette méthode du fait que celui qui l'a jamais vu, et bien y capte que dalle à ce qu'on fait comme calculs et pourquoi ça marche)
Enfin les 3 dernières lignes du tableau correspondent à la division de (a-1)x²+(a^2-a^4)x+(a^6-a^5) [qui est le résultat obtenu lors de la première division] par (x-a^2).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
