Bonjour, serait-il possible que quelqu'un explique la méthode Cardan ? svp.
J'ai un exercice qui consiste à résoudre :
x^3+3x²+15x-99 = O (E)
Elles se ramène à une équation du type : X^3+pX+q
il faut apparemment déterminer les réels a, p et q. (a=1 ; p=12 ; q=-112).
Puis, poser X = x+a. L'eq devient X^3 +12X-112=0 (E1)
On résout ensuite E1 :
on pose X= u+v
et je bloque sur :
Montrer que s'il existe des réels u et v vérifiant le système (S) alors u+v est solution de l'équation E1
S { u^3 + v^3 = 112
{ u^3v^3= -64
Comment fait-on ?
Méthode Cardan. Eq 3eme degré
5 messages
- Page 1 sur 1
Sve@r a écrit:http://fr.wikipedia.org/wiki/M%C3%A9thode_de_Cardan
Merci, j'ai déjà regardé, mais je ne comprends pas... ><
Comment, à partir du système, on peut avoir u+v solution de l'eq ? E1
Salut,
heureux de pouvoir te répondre car j'avais quelques questions perso à ce sujet !
pour la méthode:
i) on se ramène à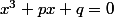
par une translation X=x+k
ii) on pose x=u+v
(u+v)=0) en développant selon le binome
en développant selon le binome
iii)
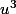 et
et 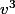 vérifient
vérifient

d'où une équation du second degré vérifiée par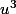 et
et 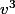

de
dans le pire des cas , quand l'angle n'est pas trisectable à la règle et au compas par exemple
on obtient par cette méthode sous forme trigo (il faut bien extraire la racine cubique complexe
sous forme trigo (il faut bien extraire la racine cubique complexe  )
)
d'où=\frac{1}{3} arctan(\theta))
je ne vois pas trop ce que la méthode apporte dans ce cas, à part situer les racines dans le plan complexe..
disons que trouver une expression rationnelle de l'argument de u en fonction des coordonnées de Y
est aussi difficle que de résoudre l'équation initiale
heureux de pouvoir te répondre car j'avais quelques questions perso à ce sujet !
pour la méthode:
i) on se ramène à
par une translation X=x+k
ii) on pose x=u+v
iii)
d'où une équation du second degré vérifiée par
de
dans le pire des cas , quand l'angle n'est pas trisectable à la règle et au compas par exemple
on obtient par cette méthode
d'où
je ne vois pas trop ce que la méthode apporte dans ce cas, à part situer les racines dans le plan complexe..
disons que trouver une expression rationnelle de l'argument de u en fonction des coordonnées de Y
est aussi difficle que de résoudre l'équation initiale
mathelot a écrit:Salut,
heureux de pouvoir te répondre car j'avais quelques questions perso à ce sujet !
pour la méthode:
i) on se ramène à
par une translation X=x+k
ii) on pose x=u+ven développant selon le binome
iii)et
vérifient
d'où une équation du second degré vérifiée paret
de
dans le pire des cas , quand l'angle n'est pas trisectable à la règle et au compas par exemple
on obtient par cette méthodesous forme trigo (il faut bien extraire la racine cubique complexe
)
d'où
je ne vois pas trop ce que la méthode apporte dans ce cas, à part situer les racines dans le plan complexe..
Je suis vraiment mais vraiment désolée, mais l'exercice est fait pour qu'on "découvre la méthode". Du coup, on ne sait rien du tout dessus. Et c'est un peu incompréhensible pour moi les quelques lignes que tu as mise...
Déja, je ne voit pas d'où sort le -p^3 / 27...
D"accord avec le II mais I et III ?
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
