Bonjour chère communauté de Maths :we: !
Voila un p'tit exercice de maths , que je trouve personnellement simple mais un vrai casse-tête !
Trouvez tous les nombres entiers naturels x et y tels que :
x-y=x^2+xy+y^2
C tout :stupid_in
Cordialment :lol3:
En même temps facile et compliqué ...
5 messages
- Page 1 sur 1
salut
 + y^2 + y = 0) est un trinome du second degré en x dont le discriminant est :
est un trinome du second degré en x dont le discriminant est :
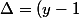^2 - 4(y^2 + y) = ... = 4 - 3(y + 1)^2)
pour avoir des solutions entières ce discriminant doit donc non seulement être positif mais aussi être un carré parfait ....
ce qui n'est le cas que pour y = 0 ou y = -1 ....
:lol3:
pour avoir des solutions entières ce discriminant doit donc non seulement être positif mais aussi être un carré parfait ....
ce qui n'est le cas que pour y = 0 ou y = -1 ....
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 115 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
