Mauvais raisonnement ?

[Anonyme]

Bonjour,

Je suis tombe aujourd'hui sur un exercice d'olympiade. Je sais comment le resoudre j'ai meme le corrige donc je ne cherche pas de reponses ni meme d'indication sur la facon de le resoudre. J'ai essaye de le resoudre d'une maniere differente et j'etais sur que mon idee etait bonne mais en fin de demonstration je trouve qu'il n'y a pas de solution ce qui n'est pas vrai.

Voici l'enonce :

Enoncé. (Olympiades Académiques-sujet national-exercice1-2003)
Les pages d’un livre sont numérotées de 1 à n ( on rappelle que la page numérotée 1 est
toujours une page de droite). On additionne les numéros de toutes les pages et on trouve un
total égal à 2003. Mais deux pages numérotés sont restées collées et leurs numéros n’ont pas
été comptés.
Quels sont le nombre de pages du livre et les numéros des pages collées ?

Ma demonstration:

Soit le nombre de page du livre et et les deux pages collees.







donc a rejette donc

Or:

Donc :

Voila j'aimerais savoir quelle est l'origine de cette absurdite
Pourquoi j'ai obtenu un resultat faux ?

Edit c'est bon l'erreur est corrige plus d'absurdite
Merci

[Sa Majesté]

Salut

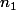
Tu t'es trompé dans ton calcul quand tu as remplacé dans l'égalité

Si tu reprends ton calcul tu tombes sur une équation triviale qui n'amène rien

Il vaut mieux se concentrer sur la racine qui doit être un entier

[Ericovitchi]

j'ai du mal à comprendre ton raisonnement quand tu réinjecte n(n+1)-8k=4008. en fait tu te mords la queue.
Moi j'aurais cherché quand est-ce que 1+4(8k+4008) est un carré. Par exemple :
si k=11 delta =128
si k=147 delta = 144
si k=221 delta = 152

[Anonyme]

Ah oui effectivement on trouve 0=0
Merci beaucoup

[Anonyme]

j'ai du mal à comprendre ton raisonnement quand tu réinjecte n(n+1)-8k=4008. en fait tu te mords la queue.

est ce toujours le cas ?
est ce que reinjecter l'equation en elle ne sert toujours a rien ?

Moi j'aurais cherché quand est-ce que 1+4(8k+4008) est un carré. Par exemple :
si k=11 delta =128
si k=147 delta = 144
si k=221 delta = 152

C'est moi maintenant qui a du mal a comprendre ton raisonnement :zen:
pourquoi un carre ?

[Ericovitchi]

pour que n soit un nombre entier, il faut bien que ce qu'il y a sous la racine soit un carré, non ?

D'ailleurs c'est pire que ça, il faut que soit entier

k=3 n=63 petit bouquin mais ça marche
k=19 n=64 petit bouquin mais ça marche
k=138 n =71 ca va pas car k > n
k=156 n=72 idem
et tous les autres après aussi

[Anonyme]

pour que n soit un nombre entier, il faut bien que ce qu'il y a sous la racine soit un carré, non ?

En effet et on continue comment ?