Matrices Terminale ES spé Maths.

[EJE38]

Bonjour,
J'ai un exercice à faire et je n'y comprend pas un mot.. Pourriez vous me diriger sur le chemin à suivre car je n'arrive même pas a entamer cet exercice. Je ne comprends pas grand chose aux systèmes et à la spé maths en général ...



Merci de votre aide.


[Edit : Je viens de tenter quelque chose, ça me paraît faux mais je vous met quand même ...

(bx + c + (d/x)) / x^2 = a
(ax^2 + c = (d/x)) / x = b
ax^2 + bx + d/x = c
(ax^2 + bx + c ) x = d

Voilà ... Mais je suis pas sûre du tout, j'ai honte ... :help: ]

[Tiruxa]

Bonjour,

En fait tu as zappé ce qui est écrit dans l'énoncé (3eme ligne)

Par exemple, dire que la courbe passe par F(1;0) cela signifie que f(1)=0.

Donc en remplaçant x par 1 dans f(x), on a :

f(1)=a+b+c+d

D'où la première équation a+b+c+d = 0

Faire de même pour F, G et H tu auras alors 4 équations à 4 inconnues.

[EJE38]

Ah oui merci beaucoup !
Je vais faire tout ça de suite :)

Donc :

E(-1) = -40 d'où a - b + c - d = - 40

F(1) = 0 d'où a + b + C + d = 0

G(2) = 11 d'où 4a + 2b + c + 0,5d (ou d/2) = 11

H(7) = 216 d'où 49a + 7b + c + d/7 = 216

Et là je les mets sous Forme matricielle :

Nous avons un système de 4 équations à 4 inconnues d'où :

A =
1 -1 1 -1
1 1 1 1
4 2 1 0,5
49 7 1 1/7

Le 1/7 est bon ??

B=
{-40}
{ 0 }
{ 11 }
{216 }

X = { a b c d } (en colonne)

Et la solution est donc :
(A)^-1 (B) =
4
6
-24
14

D'où F(x) = 4x^2 + 6x -24 + 14/x

Merci beaucoup tu m'enlève une épine du pied !!

[Suite]

F'(x) = 14/x^2 + 8x + 6

(x - 1) (4x^2 + 7x + 7)
= 4x^3 + 7x^2 + 7x - 4x^2 - 7x - 7
= 4x^3 + 3x^2 - 7

D'où
4x^3 + 3x^2 - 7 = (x - 1) (4x^2 + 7x + 7)

[Tiruxa]

C'est bien, mais tu as une erreur sur f'(x).

la dérivée de la fonction x -> 1/x est la fonction x-> -1/x²

Donc f'(x) = 8x+6-14/x²

à réduire au même dénominateur...

[EJE38]

Ah oui c'est une erreur de frappe je l'avais fait merci :)

Réduit au même dénominateur ça nous fait .... hum.. 8x + 6 -14 * (-x^2) ??
Pas sure là ...

[Tiruxa]

Ah oui c'est une erreur de frappe je l'avais fait merci

Réduit au même dénominateur ça nous fait .... hum.. 8x + 6 -14 * (-x^2) ??
Pas sure là ...

Non voici par exemple 8 mis au denominateur x² :

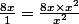
[EJE38]

Ah donc je met tout sur x^2 ?

On a donc ( 8x^3 + 6x^2 - 14 ) / x^2 ?
Merci de ton aide.

[Tiruxa]

Ah donc je met tout sur x^2 ?

On a donc ( 8x^3 + 6x^2 - 14 ) / x^2 ?
Merci de ton aide.

Oui mais ce n'est pas fini mets 2 en facteur au numérateur .

Que remarques tu ?

[EJE38]

Au final on retrouve 4x^3 + 3x^2 - 7 enfin je crois ?
D'où la fin de l'exercice.

[Tiruxa]

Oui c'est bien ça.
La fin sert pour l'étude du signe de f' mais elle permet aussi de se rendre compte que tout ce qui précède est juste (ou faux si on s'est trompé...)

[EJE38]

D'accord merci beaucoup !! :)