Bonjour à tous, alors voilà dans deux exercices différents je bloque sur la dernière et même question. Voici les exercices :
Ex1: on considère la suite (un) définie U0=1 et par la relation Un+1=Un+3n au carré+9n+7 pour tout entier naturel n.
1) calculer U1, U2, U3, U4, U5. Résultat: U1=8 , U2=27,U3=64, U4=125, U5=216
2) conjecturer l'expression de (Un) pour tout n. résultat: Un= (n+1)* (n+1)au carré
3) démontrer votre conjecture
C'est donc la question trois que je n'arrive pas
Ex2: On considère la suite (un) définie par U0=1 et par la relation Un+1= Un/ 1+2Un pour tout entier naturel n.
1) calculer U1, U2, U3, U4, U5. Résultat: U1=1/3 , U2=1/5 , U3=1/7 , U4=1/9 , U5=1/1
2) conjecturer l'expression de (Un) pour tout n. Résultat: Un= 1/ n+(n+1)
3) démontrer votre conjecture
C' est donc également la question 3) que je n'arrive pas aidez moi svp merci
Maths Suites niveau 1S
9 messages
- Page 1 sur 1
Re: Maths Suites niveau 1S
Désolé, mais vu que le principe de la démonstration par récurrence est au programme de Terminale, en 1ère je ne vois pas comment on peut faire ...
Re: Maths Suites niveau 1S
En mathématique, une conjecture est une proposition que l'on pense juste mais que personne n'a pu démontrer ou réfuter;
Ici on vous demande donc de proposé ce que vous pensez de cette suite, si elle est croissante, décroissante ou constante... à vous de trouver désormais.
J'espère que je vous ai été utile.
Bien à vous
Ici on vous demande donc de proposé ce que vous pensez de cette suite, si elle est croissante, décroissante ou constante... à vous de trouver désormais.
J'espère que je vous ai été utile.
Bien à vous
Re: Maths Suites niveau 1S
Ca se démontre sans recourrir à une récurrence mais ça suppose que l'on connaît l''expression de la somme de n premiers entiers et de la somme des carrés des n premiers entiers.
On écrit les n + 1 relations pour n variant de 0 à n :



........................
^2+9(n-1)+7)

On additionne ces n+1 relations (somme télescopique), il vient :

Or on sait (en première ???) que :
(2n+1)}{6})
}{2})
On a donc(2n-1)}{6}+3\frac{n(n-1)}{2} +7n=\frac{n}{2}[(n-1)(2n-1)+9n(n-1)+14n])
On arrive à de la forme
de la forme ^3)
Soit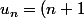^3)
On écrit les n + 1 relations pour n variant de 0 à n :
........................
On additionne ces n+1 relations (somme télescopique), il vient :
Or on sait (en première ???) que :
On a donc
On arrive à
Soit
Re: Maths Suites niveau 1S
Merci bcp mais donc comment je fais pour la même question mais de l'ex 3 ?
Re: Maths Suites niveau 1S
Plus court peut être:
U(n+1) - Un = (n+2)^3 - (n+1)^3
Tu développes ça et tu devrais retomber sur ton polynome.
U(n+1) - Un = (n+2)^3 - (n+1)^3
Tu développes ça et tu devrais retomber sur ton polynome.
Re: Maths Suites niveau 1S
Pour 3) de l'Ex 2, tu supposes vrai Un=1/(2n+1) et tu calcules Un/U(n+1) qui doit donner 2Un+1.
Par exemple.
Par exemple.
Re: Maths Suites niveau 1S
Pour l'ex 3 j'ai fait ce que vous m'avez dit j'ai donc trouvé 2(UN)+1 mais je ne vois pas en quoi cela démontre la conjecture
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
