Maths spé sujet bac (asie 99)

[mimi_chokoolat]

[FONT=Comic Sans MS]bonjour a tous!alors voila je suis face a un sujet de bac et en fait je bloque à certaines questions....

1. On considère l'équation (E) : 8x+5y = 1, où est un couple de nombres
entiers relatifs.
a. Donner une solution particulière de l'équation (E).OK
b. Résoudre l'équation (E).OK

2. Soit N un nombre naturel tel qu'il existe un couple (a ; b) de nombres entiers
vérifiant : N = 8a +1(systeme)
N = 5b +2
a. Montrer que le couple (a ; -b) [COLOR=Red](je me demande si c'est pas (a; b) nan? coquile??) est solution de (E).
b. Quel est le reste, dans la division de N par 40 ?BLOKEE(jai pas compris :embarras:)


3. a. Résoudre l'équation 8x +5y = 100, où (x ; y) est un couple de nombres
entiers relatifs. en fait jai trouver (10;2) ms au pifometre lol

b. Au VIIIe siècle, un groupe composé d'hommes et de femmes a dépensé
100 pièces de monnaie dans une auberge. Les hommes ont dépensé 8
pièces chacun et les femmes 5 pièces chacune. Combien pouvait-il y
avoir d'hommes et de femmes dans le groupe ? bah 10 homme et 4 femmes mais pareil c'est au pif...en fait si je prouve la question précédente bah cette question là est trouvée.

merci par avance pr votre aide. [/COLOR][/FONT]

[mimi_chokoolat]

:doh: bah dites donc sa veut dire qu epour linstant jai pas le niveau du bac :doh:

[nxthunder]

Soit N un nombre naturel tel qu'il existe un couple (a ; b) de nombres entiers
vérifiant : N = 8a +1(systeme)
N = 5b +2
a. Montrer que le couple (a ; -b) (je me demande si c'est pas (a; b) nan? coquile??) est solution de (E).

Nan Nan cest bien ( a ; -b ) En effet :

On sait que

N= 8a+1
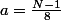
N=5b+2

On remplace x par a et y par -b :

8()+5()

N-1-N+2 = 1

Donc le couple (a ; -b ) est bien solution de E

b)
Tu traites le cas ou 40 | 8a+1
et le cas ou 40 | 5b+2
enfin j'pense ^^

[luigi]

Hello !

3a) NORMAlement, dans la question 1, tu as trouvé un couple solution particulier (x0,y0) vérifiant 8x + 5y = 1. Pour résoudre 8x + 5y = 100, une solution particulière est (100 x0, 100 y0). Ensuite, la solution générale se trouve dans ton cours.

3b) Si tu fais x = nombre d'hommes et y = nb de femmes. Tu retrouves l'équation 8x + 5y = 100. La réponse est finalement la solution générale de 3a.

[mimi_chokoolat]

ui dans la question 1 jai trouver le couple (2;3) donc sa devient 200 et 300?

[luigi]

En fait, le couple de la question 1 est (2,-3) donc ça devient 200 et -300 comme tu l'as bien compris.