Maths spe cosinus et sinus

[Benoît]

Bonjour,
j'ai un exercice que je ne comprends pas.
Si quelqu'un peut m'aider ca serait super


creer lien de telechargement direct

[Pisigma]

Bonjour,

[WillyCagnes]

bjr,

mettre 7/2 en facteur, ensuite tu reconnaitras des sin et cos remarquables connus

[Benoît]

Bonjour,

Merci beaucoup, mais dans l'énoncé on demande un + pour la pulsation et le déphasage,
ce n'est pas gênant si c'est un moins ?

[mathelot]

non, il s'agit d'utiliser cos(a+b) =cosa cosb-sina sinb

[Benoît]

Ah d'accord je vois, et donc du coup je ne comprends pas a quoi correspondent la tension maxi, la pulsation et le déphasage dans ce qu'a écrit Pisigma

[Pisigma]

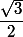
il suffit de trouver l'angle donc le cosinus vaut et le sinus vaut

et tu auras