Dm de maths seconde !! vecteurs et cercle circonscrit

[hakim88style]

Bonjour, j'éprouve des difficultés a résoudre cet exercice de maths : :help:

Le repère (O; vecteur i ; vecteur j) est orthonormal. Le triangle ABC est défini par les points A(-3;0), B (6;3) et C(1;8). on veut déterminer les coordonnées (x;y) du point K, centre du cercle circonscrit à ABC.

1. Dire que K est le centre du cercle circonscrit équivaut à dire que K est équidistant de A,B et C et donc que:

KA²=KB²
KB²=KC²

Calculez KA², KB² et KC² en fonction de x et y puis écrivez les égalités traduisant cette condition

2. Déduisez-en que : 3x+y=6
-x+y=2

3. Calculez les coordonnées de K

EN vous remerciant d'avance...

[oscar]

Bonjour

K est à l' intersection des médiatrivces de [AC] et [AB]
1) médiatrice de [ÂB]
miliau M ( ( -3+6)/2; (0+3)/2) = (3/2; 3/2)
Pente de AB: 3/9= 1/3
y =x/3 +k( d1)
M sur d1=> 3/2= 3/6+k=> k =1
d1: y = x/3 +1
2)
Médiatrice de AC ^procéde
3) d1 inter d2 = K

[Florélianne]

Bonjour ,
La réponse est sans doute bonne mais ne répond pas aux questions posées...
j'ai préparé la réponse mais je ne sais toujours pas insérer... alors que fais-je de ma capture ? rien, elle va rejoindre tout ce que j'ai fait pour rien, parce que personne ne le réclame...
Bonne soirée

[Timothé Lefebvre]

Bonsoir Florélianne :)

La réponse se trouve dans le lien ci-dessous (Comment insérer une image sur le forum), j'espère qu'il pourra t'aider !

Amicalement.

[hakim88style]

Bonjour ,
La réponse est sans doute bonne mais ne répond pas aux questions posées...
j'ai préparé la réponse mais je ne sais toujours pas insérer... alors que fais-je de ma capture ? rien, elle va rejoindre tout ce que j'ai fait pour rien, parce que personne ne le réclame...
Bonne soirée

Bonsoir Florélianne !! Je te suis pas :hein: !! Apparement tu aurais résolu mon exercice mais tu n'as pas su l'insérer sur le topic ?? Cependant Timothé t'aurais indiqué ce qu'il fallait faire !! Et je te serais très reconnaissant de m'aider !! Merci

[oscar]

Ta méthode
KA² = KB²=> (x+3)² +-y² = (x-6)² + ( y-3)²<=>
x² + 6x +9+y² = x² -12x+36 +y² -6y+9<=> 18x+6y-36=0<=> 3x +y -6=0(1)

KB² =KC²=>(x-6)² +(y-3)²=(x-1)²+(y-8)²<=>-14x+10y-20=0<=>)
7x-5y+10=0(2)
résous le système (1) (2)

Vérifie mes calculs!

[Florélianne]

Bonsoir,
J'avais déjà étudié cette page... c'est tout en anglais ! et j'ai toujours été nulle en anglais...
J'ai fait ce que j'ai pu! pas certaine d'y être arrivé !
Bonne soirée

[mathelot]

Bj,

Il y a une relation entre un triangle ABC et son triangle médian
A'B'C' où A' est le milieu de [BC],B' est le milieu de [AC],
C' est le milieu de [AB].

En particulier A'B'C' a des côtés parallèles à ceux de ABC,
le centre du cercle circonscrit O de ABC est l'orthocentre de A'B'C',
A'B'C' et ABC ont même centre de gravité G.

Comme , en seconde, il est bien connu que


que G a des coordonnées faciles à calculer,
H aussi a des coordonnées faciles à calculer (surtout ses coordonnées
projectives (tanA,tanB,tanC),

qu'un triangle ABC est triangle médian d'un sur-triangle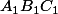 ,que l'on peut appliquer la formule d'Euler dans plusieurs triangles,
en changeant O en H', y-a-t-il moyen d'obtenir une formule agréable pour les coordonnées du centre du cercle circonscrit ?

par exemple, si l'on pouvait exprimer agréablement
où H et H' sont deux orthocentres de triangles alter-médians (je forge cette expression)