Dm de maths: Quelques problemes

[problememaths]

Bonjour,

Comme vous vous en doutez, j'ai un problème de maths, enfin plusieurs...
Voila, pour la rentrée nous avons un Dm de maths a rendre comportant 3 exercices... Et j'aurais quelques questions dans chaque exo.

Exercice 1
J'ai plutôt bien réussi cet exercice, juste un petit soucis a la dernière question, comment résoudre:
[INDENT]
[e(x) - e(-x)] / 2 = 3
e(x) - e(-x) = 6[/INDENT]

j'ai pensé a utiliser ln mais c'est une soustraction...

Exercice 2

[INDENT]g(t) = [1-e(-t)] ln(t)
g(0) = 0

2. Démontrer que g est continue sue ]0;1]. Etudier la derivabilité de g sur ]0;1][/INDENT]

Si je me contente d'étudier la dérivabilité et la continuité de g(t) en 0 et 1 cela suffit ?

Exercice 3

[INDENT]Nous voulons résoudre l'équation (1) cos(x) + cos(2x) + cos(3x) = 0

1. Montrer que le membre de gauche de l'équation (1) est la partie réelle d'un nombre complexe Z, que l'on precisera.[/INDENT]

Je n'arrive pas a démarrer car je ne comprends pas cette question...


Merci de votre aide a tous :ptdr:

[Huppasacee]

Bonjour

pour l'exercice 1 , tu multiplies tout par
et ensuite poser
= X ( remarquer que X >0 )

[Huppasacee]

exercice 3

poser
z = cosx + i sinx

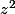
D'après la formule de Moivre, que vaut , et ?

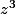
ensuite , fais le lien avec la question

[problememaths]

Ok merci pour l'exercice 1 et 3...

Exercice 3

Nous voulons résoudre l'équation (1) cos(x) + cos(2x) + cos(3x) = 0

1. Montrer que le membre de gauche de l'équation (1) est la partie réelle d'un nombre complexe Z, que l'on precisera

[INDENT]J'ai donc trouvé
Z = cox (x) + cos (2X) + cos (3x) + i[sin x + sin(2x) + sin(3x) ][/INDENT]

2. Ecrire Z comme la somme des 3 premiers termes d'une suite geometrique et en déduire que Z = e(ix) [ (1-e(i3x)) / (1-e(ix)) ]

[INDENT]La j'ai trouvé[/INDENT]

3. Factoriser par e(i 3x/2) le numerateur et par e(i x/2) le denominateur pour faire apparaitre les formules d'Euler...

[INDENT]J'ai trouvé

Z = e(ix) [ ( 2 / [e(i 3x/2) - e(-i 3x/2)] ) ( [e(i 3x/2) - e(-i 3x/2)] / 2 ) ][/INDENT]

4. Montrer que Re(Z) = cos(2x) [sin(3x/2) / sin(x/2)]

[INDENT]J'ai commencé avec

Re(Z) = cos(x) + cos(2x) + cos(3x)

en factorisant j'arrive a:

Re(Z) = cos(2x) [ ( e(ix) + e(-ix) + e(i2x) + e(-i2x) + e(i3x) + e(-i3x) ) / ( e(i2x) + e(-i2x) ) ]

Et la, je trouve pas [/INDENT] :mur:


Merci de votre aide
(si quelqu'un pouvais aussi jeter un petit coup d'oeil a l'exercice 2 du premier message svp :we: )

[Florélianne]

Exercice 2[indent]g(t) = [1-e^(-t)] ln(t)
g(0) = 0

2. Démontrer que g est continue sue ]0;1]. Étudier la dérivabilité de g sur ]0;1][/indent]
Si je me contente d'étudier la dérivabilité et la continuité de g(t) en 0 et 1 cela suffit ?
Je ne comprends pas ce qui te gène. g(t) est continue sur ]0 ; 1] comme somme (algébrique) et produit de fonctions continues sur ]0 ; 1]
de même pour dérivable
on ne te demande pas de le prouver en 0 puisque c'est sur ]0 ; 1]
et 1 n'a rien de spécial ni pour la continuité ni pour la dérivabilité : e^(-1) existe et la fonction exponentielle est définie, continue et dérivable sur tout IR (-1 compris !)
quand à la fonction ln elle est définie continue et dérivable sur ]0 ; +oo[ donc aussi pour 1

si on te demandait de prouver que g est continue et dérivable sur [0 ; 1] il ne te resterait qu'à étudier le cas t=0 c'est à dire :
lim (t-> 0) [1-e^(-t)] ln(t)
et si g est continue en 0 lim(t->0)[size=4][[/size][1-e^(-t)] ln(t)-0]/(x-0)
sinon inutile!
Bonne soirée

[Huppasacee]

2. Ecrire Z comme la somme des 3 premiers termes d'une suite geometrique et en déduire que Z = e(ix) [ (1-e(i3x)) / (1-e(ix)) ]

la suite de tes calculs erronée

La mise en facteur conseillée nous donne plutôt :




Rappel :d'après les formules d'Euler :

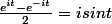
[problememaths]

Merci pour tout...

C'est bon j'ai tout trouvé !

:ptdr: