DM de maths niveau 1ereS
19 messages
- Page 1 sur 1
DM de maths niveau 1ereS
Bonjours !
J'ai un DM a rendre et notre prof ne nous a pas appris comment résoudre un des exercice donc je ne sais pas comment faire... C'est une inéquation de valeurs absolues, est ce que quelqu'un peu m'aider et m'expliquer comment cela fonctionne ? merci beaucoup !
voici l'inéquation :
|3-x| > |x+3|-2|x|
J'ai un DM a rendre et notre prof ne nous a pas appris comment résoudre un des exercice donc je ne sais pas comment faire... C'est une inéquation de valeurs absolues, est ce que quelqu'un peu m'aider et m'expliquer comment cela fonctionne ? merci beaucoup !
voici l'inéquation :
|3-x| > |x+3|-2|x|
Re: DM de maths niveau 1ereS
Bonjour
Tu peux distinguer plusieurs cas selon la position de x par rapport à 3, 0 et -3.
Tu peux faire un tableau.
Tu remplaces ton inéquation par 4 inéquations faciles à résoudre.
Tu peux distinguer plusieurs cas selon la position de x par rapport à 3, 0 et -3.
Tu peux faire un tableau.
Tu remplaces ton inéquation par 4 inéquations faciles à résoudre.
Re: DM de maths niveau 1ereS
Comment ça ? je n'ai jamais vue tout ça, on a jamais vue comment résoudre une inéquation avec des valeurs absolues pour l'instant, donc je ne sais absolument pas comment remplacé par d'autres inéquations etc 

Re: DM de maths niveau 1ereS
Salut,
Vu que tu ne pose pas la question de savoir ce qu'est une valeur absolue, ben j'en déduit que tu connait la définition.
Et de connaitre la définition de ce qu'est une valeur absolue est largement suffisant pour faire un exercice de ce type.
|3-x|, ça signifie quoi ? et |3+x| ? et |x| ?
Vu que tu ne pose pas la question de savoir ce qu'est une valeur absolue, ben j'en déduit que tu connait la définition.
Et de connaitre la définition de ce qu'est une valeur absolue est largement suffisant pour faire un exercice de ce type.
|3-x|, ça signifie quoi ? et |3+x| ? et |x| ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: DM de maths niveau 1ereS
la seul chose qu'on sait sur la valeur absolue, c'est ça définition ( x --> |x|) son domaine de définition, son sens de variation, sa partié/impartié et c'est tout on connais que ça 
ducoup bah... |3-x| le seul truc que je peux te dire c'est que sur ]-infini ; 3] elle est décroissante puis croissante sur [3 ; +infini[ , pour |3+x| c'est décroissant sur ]-infini ; -3] et croissante sur [-3 ; +infini[ et pour |x| décroissant sur R- et croissant sur R+, c'est le seul truc que je peux dire avec ce qu'on a appris, et encore je suis pas sur que ce soit juste

ducoup bah... |3-x| le seul truc que je peux te dire c'est que sur ]-infini ; 3] elle est décroissante puis croissante sur [3 ; +infini[ , pour |3+x| c'est décroissant sur ]-infini ; -3] et croissante sur [-3 ; +infini[ et pour |x| décroissant sur R- et croissant sur R+, c'est le seul truc que je peux dire avec ce qu'on a appris, et encore je suis pas sur que ce soit juste

Re: DM de maths niveau 1ereS
Salut !
Ce qui te gêne, ce sont les valeurs absolues, donc pour s'en débarrasser, il faut revenir à la définition de ce que c'est que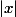 :
:
-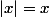 si
si 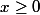 et,
et,
-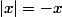 si
si 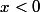 .
.
Ici, c'est pareil, de façon général, pour une certaine expression) (dépendant de
(dépendant de  ), tu auras :
), tu auras :
-|=E(x)) pour tous les
pour tous les  vérifiant
vérifiant  \ge 0) et,
et,
-|= - E(x)) , pour tous les
, pour tous les  vérifiant
vérifiant  <0) .
.
Il faut donc trouver pour quelles valeurs de x, on a \ge 0) ou
ou  <0) : cela revient donc à étudier le signe de
: cela revient donc à étudier le signe de ) .
.
Etudie donc les signes de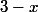 ,
, 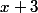 et
et  suivant les valeurs du réel
suivant les valeurs du réel  , pour en déduire une expression de
, pour en déduire une expression de  ,
,  et
et 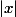 .
.

Ce qui te gêne, ce sont les valeurs absolues, donc pour s'en débarrasser, il faut revenir à la définition de ce que c'est que
-
-
Ici, c'est pareil, de façon général, pour une certaine expression
-
-
Il faut donc trouver pour quelles valeurs de x, on a
Etudie donc les signes de
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: DM de maths niveau 1ereS
merci beaucoup, juste (oui excuse moi  ) pourrais-tu me faire un exemple avec un E(x) (pas avec mes valeurs hein, juste que je comprenne bien ^^")
) pourrais-tu me faire un exemple avec un E(x) (pas avec mes valeurs hein, juste que je comprenne bien ^^")
 ) pourrais-tu me faire un exemple avec un E(x) (pas avec mes valeurs hein, juste que je comprenne bien ^^")
) pourrais-tu me faire un exemple avec un E(x) (pas avec mes valeurs hein, juste que je comprenne bien ^^")Re: DM de maths niveau 1ereS
Ok par exemple avec =x^2-1) .
.
A l'aide d'un tableau de signe (ou alors si tu le sais déjà), tu as :
- lorsque
lorsque  et,
et,
- lorsque
lorsque 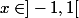 .
.
Donc :
- si alors
alors  et,
et,
- si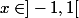 alors
alors =1-x^2) .
.

A l'aide d'un tableau de signe (ou alors si tu le sais déjà), tu as :
-
-
Donc :
- si
- si
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: DM de maths niveau 1ereS
Mais une fois que j'aurai fais ça pour 3-x x+3 et x, je fais quoi avec mon inéquation ? 

Re: DM de maths niveau 1ereS
Qu'obtiens-tu ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: DM de maths niveau 1ereS
j'obtiens :
pour 3-x :
3-x >(ou egale) 0 lorsque x appartient a ]-infini ; 3]
3-x < 0 lorsque x appartient a ]3 ; +infini[
pour x+3 :
x+3 >(ou egale) 0 lorsque x appartient a [-3 ; +infini[
x+3 < 0 lorsque x apparient a ]-infini ; -3]
pour x :
x>(ou egale) 0 lorsque x appartient a [0 ; +infini[
x<0 lorsque x appartient a ]-infini ; 0[
pour 3-x :
3-x >(ou egale) 0 lorsque x appartient a ]-infini ; 3]
3-x < 0 lorsque x appartient a ]3 ; +infini[
pour x+3 :
x+3 >(ou egale) 0 lorsque x appartient a [-3 ; +infini[
x+3 < 0 lorsque x apparient a ]-infini ; -3]
pour x :
x>(ou egale) 0 lorsque x appartient a [0 ; +infini[
x<0 lorsque x appartient a ]-infini ; 0[
Re: DM de maths niveau 1ereS
xsylv1z a écrit:j'obtiens :
pour 3-x :
3-x >(ou egale) 0 lorsque x appartient a ]-infini ; 3]
3-x < 0 lorsque x appartient a ]3 ; +infini[
pour x+3 :
x+3 >(ou egale) 0 lorsque x appartient a [-3 ; +infini[
x+3 < 0 lorsque x apparient a ]-infini ; -3]
pour x :
x>(ou egale) 0 lorsque x appartient a [0 ; +infini[
x<0 lorsque x appartient a ]-infini ; 0[
Ok ; maintenant le problème qui se pose, c'est d'écrire la fonction
Ecrit
écrit
écrit
écrit
Résoudre alors ton équation revient à résoudre f(x)>0, ce qui revient à résoudre les quatre inéquations obtenues précédemment en faisant attention : pour chaque inéquation x appartient déjà à un intervalle qui n'est pas R tout entier.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: DM de maths niveau 1ereS
donc les inéquations sont :
3-x-(-x-3)-2 quand x appartient a ]-infini ; -3[
3-x-x+3-2x quand x appartient a [-3 ; 0[
3-x-x+3+2x quand x appartient a [0 ; 3[
-3+x-x+3+2x quand x appartient a [3 ; +infini[
c'est bien ça ?
3-x-(-x-3)-2 quand x appartient a ]-infini ; -3[
3-x-x+3-2x quand x appartient a [-3 ; 0[
3-x-x+3+2x quand x appartient a [0 ; 3[
-3+x-x+3+2x quand x appartient a [3 ; +infini[
c'est bien ça ?
Re: DM de maths niveau 1ereS
Il manque un x :
Si tu l'écris comme ça, c'est faux : il manque des parenthèses :
f(x)=3-x-(-x-3)-2x quand x appartient a ]-infini ; -3[
f(x)=3-x-(x+3)-2x quand x appartient a [-3 ; 0[
f(x)=3-x-(x+3)+2x quand x appartient a [0 ; 3[
f(x)= -(3+x)-(x+3)+2x quand x appartient a [3 ; +infini[.
De façon générale, quel que soient deux réels a,b, on n'a pas -a+b=-(a+b)
Maintenant, il te faut résoudre f(x)>0 sur les quatre différents intervalles.
xsylv1z a écrit:donc les inéquations sont :
3-x-(-x-3)-2x quand x appartient a ]-infini ; -3[
3-x-x+3-2x quand x appartient a [-3 ; 0[
3-x-x+3+2x quand x appartient a [0 ; 3[
-3+x-x+3+2x quand x appartient a [3 ; +infini[
c'est bien ça ?
Si tu l'écris comme ça, c'est faux : il manque des parenthèses :
f(x)=3-x-(-x-3)-2x quand x appartient a ]-infini ; -3[
f(x)=3-x-(x+3)-2x quand x appartient a [-3 ; 0[
f(x)=3-x-(x+3)+2x quand x appartient a [0 ; 3[
f(x)= -(3+x)-(x+3)+2x quand x appartient a [3 ; +infini[.
De façon générale, quel que soient deux réels a,b, on n'a pas -a+b=-(a+b)
Maintenant, il te faut résoudre f(x)>0 sur les quatre différents intervalles.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: DM de maths niveau 1ereS
merci beaucoup mais je l'es rendu tout a l'heure haha ^^
mais aucun souci, je perdrai surement quelque point pour les parenthèse mais dans tout les cas la solution c'est R (avec et sans parenthèse, enfin je pense car sur la calculette quand on trace les graphique on trouve grand R et c'est ce que j'ai trouvé) en tout cas merci beaucoup !
mais aucun souci, je perdrai surement quelque point pour les parenthèse mais dans tout les cas la solution c'est R (avec et sans parenthèse, enfin je pense car sur la calculette quand on trace les graphique on trouve grand R et c'est ce que j'ai trouvé) en tout cas merci beaucoup !
Re: DM de maths niveau 1ereS
Salut !
Désolé, mais l'ensemble des solutions n'est pas R tout entier : il suffit de prendre par exemple 0 : on n'a pas |3-0| > |0+3|-2|0|. Il me semble que c'est plutôt R\[0,3].
Désolé, mais l'ensemble des solutions n'est pas R tout entier : il suffit de prendre par exemple 0 : on n'a pas |3-0| > |0+3|-2|0|. Il me semble que c'est plutôt R\[0,3].
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: DM de maths niveau 1ereS
Si si, c'est c’est supérieur ou égale  excuse moi j'utilise pour la première fois ce forum je connaissais pas encore comment faire "de belles formules mathématiques"
excuse moi j'utilise pour la première fois ce forum je connaissais pas encore comment faire "de belles formules mathématiques" 
Re: DM de maths niveau 1ereS
Ah ok, dans ce cas là, je suis d'accord 

- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: DM de maths niveau 1ereS
en tout cas merci beaucoup ! ce forum est genial je vais en parler autour de moi ^^
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 99 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
