Maths exos terminale s

par **mathilde98** » 15 Sep 2015, 18:16

Bonjour!

Je suis en terminale s et j'ai deux exercices à faire que je ne comprends vraiment pas du tout....
Pourriez vous me donner des pistes pour continuer?

Exercice 1:
Soit n un entier naturel
a- Montrer que le reste de la division de n² par 8 ne peut être que 0, 1 ou 4 ( distinguer selon si n est pair ou impair)
b- montrer que si n est impair alors le reste de la division euclidienne de n^(4) est égal à 1.

Merci d'avance!

par **zygomatique** » 15 Sep 2015, 19:14

salut

ex1 :

a/ calcule n^2 en écrivant que n est pair ou impair ...

b/ question incomplète ....

par **mathilde98** » 15 Sep 2015, 21:22

zygomatique a écrit:salut

ex1 :

a/ calcule n^2 en écrivant que n est pair ou impair ...

b/ question incomplète ....

Déjà merci d avoir repondu:)

Pour la question b, c est toujours pour n^4 divise par 8!

Et pour la a, je l ai fait mais après je suis bloquée...
J ai mis
(2k)^2= 8q+r donc 4k^2= 8 q+r
Et après pareil quand n est impair (2k+1)^2....

par **zygomatique** » 16 Sep 2015, 13:31

n'importe quoi ...

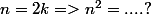
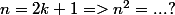
et puis on constate que ça ne suffit pas .... (quel est l'intérêt de cette indication ? :hein: )

puis on réfléchit ... et comme on veut faire une division par 8 alors écrivons

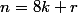
avec

puis calculons le carré de n ... et regardons ....

par **mathilde98** » 16 Sep 2015, 16:21

zygomatique a écrit:n'importe quoi ...

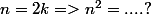
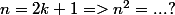
et puis on constate que ça ne suffit pas .... (quel est l'intérêt de cette indication ? :hein: )

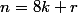
puis on réfléchit ... et comme on veut faire une division par 8 alors écrivons avec

puis calculons le carré de n ... et regardons ....

Oui c'est ce que je voulais dire mais je me suis mal exprimée...
on a donc si n est pair
n= 2k donc n*n= 4k²
si n est impair
n= 2k+1 donc n²= (2k+1)²= 4k²+4k+1

Sauf que si on nous dit la division de n² par 8 cela signifie bien qu'on a n²=8q+r non?
sauf qu'après je suis coincée car même si je remplace la valeur de n par 2k ou 2k+1 j'ai beaucoup trop d'inconnues...

par **zygomatique** » 16 Sep 2015, 16:34

oui on fait la division par 8

oui n^2 = 8k + r ... mais le pb c'est d'avoir r ....

qu'on peut avoir lorsque n est impair ... car n^2 = 4k(k + 1) + 1 et on peut conclure quelque chose ...

reste à voir le cas pair ... et je t'ai donné une idée ....

par **mathilde98** » 16 Sep 2015, 19:06

zygomatique a écrit:oui on fait la division par 8

oui n^2 = 8k + r ... mais le pb c'est d'avoir r ....

qu'on peut avoir lorsque n est impair ... car n^2 = 4k(k + 1) + 1 et on peut conclure quelque chose ...

reste à voir le cas pair ... et je t'ai donné une idée ....

donc n²=4k(k+1)+1 est ce qu'on pourrait alors dire que le reste de la division de n² par k-1 est 1? mais alors je ne vois pas trop la logique avec l'égalité de départ....

Et donc si j'essaye de suivre votre raisonnement:
quand n est pair on a n²= 4k² donc n² est divisible par 4k comme quand est n est impair...

Je suis désolée j'essaie vraiment de comprendre mais j'admets que j'ai du mal :/

par **zygomatique** » 16 Sep 2015, 19:13

que peux-tu dire du produit k(k + 1) ?

mais je vois que tu as du mal et je t'ai donné une méthode simple à 14h31 ....

par **mathilde98** » 16 Sep 2015, 19:17

zygomatique a écrit:que peux-tu dire du produit k(k + 1) ?

mais je vois que tu as du mal et je t'ai donné une méthode simple à 14h31 ....

k(k+1) ressemblerait à q dans une division euclidienne de n² par 4 avec 1 comme reste

ou alors est ce qu'on pourrait dire que
n=8q+r donc quand on met n au carré on a n²=4*2q+r et donc 2q serait k(k+1)?

Maths exos terminale s

Maths exos terminale s

Qui est en ligne