Miranda25 a écrit:j'ai essayé de faire ce que tu m'as dis sur feuille mais je ne comprend pas comment il reste 2^(n+1)-1 à la fin car même en developpant puis en simplifiant il me reste 2^(n+1) 2^0,2^3 et 2^n je dois avoir faux quelques part
je détail mon calcul(dsl pour la notation)
S=2^0+2^1+2^3+...+2^n or 2^n=2^(n+1)-2^n donc (2^1-2^0)+(2^2-2^1)+(2^3-2^2)+(2^(n+1)-2^n)
on simplifie S= les termes s'annulent entre eux sauf 2^n, 2^3,2^0 et 2^(n+1)
je pense que tous cela est faux
Je reprends à zéro mais avant tout remarque que c'est le calcul classique de S=q^0+q^1+.....q^n pour tout
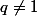
.
Ici q =2, S=1+2+2^2+.....+2^n. L'idée est de multiplier S par 2-1, puis de développer et simplifier.
Donc
S=S(2-1)=2S-S
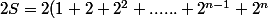=2+2^2+2^3+...+2^n+2^{n+1})
Je retire S=1+2+.....+2^n à 2S. on voit qu'on presque les m^mes termes dans 2S et S, ces termes s'éliminent mais il reste 2^{n+1}
qui est dans 2S et -1 qui qui est dans S.
i.e

j'ai pas vu ton dernier message oui c'est que tu as repris de @mathelot c'est pareil.
