DM MATHS 2 exos ( suites + proba)
30 messages
- Page 1 sur 2 - 1, 2
 DM MATHS 2 exos ( suites + proba)
DM MATHS 2 exos ( suites + proba)
Bonsoir tous le monde, j’espère que vous avez passé un bon réveillon de Noël !
J’ai un devoir maison que j´ai commencé mais depuis hier je bloque sur un exercice et sur une question.
Il y a donc un exercice sur les suites
1) montrer que pour tout n on a 2^n+1+2^n=2^n
2) on considere la somme S= 2^0+2^1+2^2+2^3+...+2^n
En réinvestissant la question 1) donner une expression simple de S en fonction de n
J’ai fais le 1) et j’ai trouvé 2^n(2-1) =2^n
Pour la 2) je ne sais pas comment faire sachant qu’un proche m’a dis que c’était une suite géométrique or je n’ai pas de cours sur les suites geometriques
Si qlq peut m’aider svp
L’exo 2 : probabilité
Un jeu a les regles suivantes : une urne contient 9 boules blanches et une boule noire. On extrait a hasard une boule de l’urne: si elle est de couleur noire le jeu se termine
Si elle est de couleur blanche on la remet dans l´urne puis on procede au tirage d’une nouvelle boule de l’urne. Le jeu se termine
1) faire un arbre de probabilités
2) on gagne 10€ si on obtient une boule noire au premier tirage. 5€ au second tirage. Sinon on perd 2€
Soit X la variable aléatoire egale au gain algebrique du joueur
a) donner la loi de probabilité de X
b) calculer l’esperance mathematique de X. Ce jeu est-il equitable ?
Pour cet exercice j’ai fais le petit 1) mais le 2 je n’y arrive pas
P(10)= ?
P(5)=?
P(-2)=?
Au depart j’avais mis p(10)=1/10 P(5)=1/10 et P(-2)=9/10 or la somme est différente de 1 est c’est impossible
J’ai un devoir maison que j´ai commencé mais depuis hier je bloque sur un exercice et sur une question.
Il y a donc un exercice sur les suites
1) montrer que pour tout n on a 2^n+1+2^n=2^n
2) on considere la somme S= 2^0+2^1+2^2+2^3+...+2^n
En réinvestissant la question 1) donner une expression simple de S en fonction de n
J’ai fais le 1) et j’ai trouvé 2^n(2-1) =2^n
Pour la 2) je ne sais pas comment faire sachant qu’un proche m’a dis que c’était une suite géométrique or je n’ai pas de cours sur les suites geometriques
Si qlq peut m’aider svp
L’exo 2 : probabilité
Un jeu a les regles suivantes : une urne contient 9 boules blanches et une boule noire. On extrait a hasard une boule de l’urne: si elle est de couleur noire le jeu se termine
Si elle est de couleur blanche on la remet dans l´urne puis on procede au tirage d’une nouvelle boule de l’urne. Le jeu se termine
1) faire un arbre de probabilités
2) on gagne 10€ si on obtient une boule noire au premier tirage. 5€ au second tirage. Sinon on perd 2€
Soit X la variable aléatoire egale au gain algebrique du joueur
a) donner la loi de probabilité de X
b) calculer l’esperance mathematique de X. Ce jeu est-il equitable ?
Pour cet exercice j’ai fais le petit 1) mais le 2 je n’y arrive pas
P(10)= ?
P(5)=?
P(-2)=?
Au depart j’avais mis p(10)=1/10 P(5)=1/10 et P(-2)=9/10 or la somme est différente de 1 est c’est impossible
Re: DM MATHS 2 exos ( suites + proba)
Bonsoir,
Pour l'exercice 1, pourrais-tu insérer l'image de l'énoncé (guide-utilisation-f41/comment-inserer-une-image-t174537.html) ou utiliser la syntaxe TEX pour mettre en forme ta formule (guide-utilisation-f41/ecrire-des-belles-formules-mathematiques-balises-tex-t70548.html)
Merci
Pour l'exercice 1, pourrais-tu insérer l'image de l'énoncé (guide-utilisation-f41/comment-inserer-une-image-t174537.html) ou utiliser la syntaxe TEX pour mettre en forme ta formule (guide-utilisation-f41/ecrire-des-belles-formules-mathematiques-balises-tex-t70548.html)
Merci
Re: DM MATHS 2 exos ( suites + proba)
Pour l'exercice 2) pourrais-tu indiquer ce que tu as déjà fait ? Éventuellement une photo ?
Re: DM MATHS 2 exos ( suites + proba)
Bonjour L'exercice 2 attention à l'écriture:
P(10) c'est pas la bonne notation.
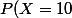=1/10=10/100 ;<br />P(X=5)=9/10\times 1/10=9/100;<br />P(X=-2)=9\10\times 9/10=81/100.)
10+9+81=100 Ok....
P(10) c'est pas la bonne notation.
10+9+81=100 Ok....
Re: DM MATHS 2 exos ( suites + proba)
Merci aviateur j’avais « juste » il fallait juste que ce soit sur 100 j’ai pas assez réfléchi visiblement
Merci bcp
Du coup ça vérifie la loi de probabilité
b) pour que le jeu soit equitable il faut que ça valent 0 du coup en faisant le calcul de l´esperance je trouve -17/100
(Dsl pour la notation) donc le jeu n’est pas equitable est-ce juste ?
Merci bcp
Du coup ça vérifie la loi de probabilité
b) pour que le jeu soit equitable il faut que ça valent 0 du coup en faisant le calcul de l´esperance je trouve -17/100
(Dsl pour la notation) donc le jeu n’est pas equitable est-ce juste ?
Re: DM MATHS 2 exos ( suites + proba)
j'ai essayé, en suivant les indications sur les liens que vous m'avez donné de mettre une photo de ce que j'ai fais ou alors changé la notation mais ça ne fonctionne pas et je ne comprends pas pourquoi.
Je suis désolé
Vous pouvez quand même m'aider ou du coup c'est gênant ?
Je suis désolé

Vous pouvez quand même m'aider ou du coup c'est gênant ?
Re: DM MATHS 2 exos ( suites + proba)
non c'est 2^(n+1)-2^n=2^n donc 2^n(2-1)=2^n
En revanche je suis sure de ce que j'ai écrit.
En revanche je suis sure de ce que j'ai écrit.
Re: DM MATHS 2 exos ( suites + proba)
Oui c'est ça. L'espérance du gain du joueur est négatif. Le jeu lui est défavorable (comme tout jeu d'argent qui se respecte)
Re: DM MATHS 2 exos ( suites + proba)
Super, merci beaucoup !
C'est possible que maintenant vous m'aidez pour la question 3 de l'exercice 1 ? svp
C'est possible que maintenant vous m'aidez pour la question 3 de l'exercice 1 ? svp
Re: DM MATHS 2 exos ( suites + proba)
S=2^(n+1) -1 ?
j'ai quitté l’école il y a un moment j'essaie de m'y remettre
j'ai quitté l’école il y a un moment j'essaie de m'y remettre
Re: DM MATHS 2 exos ( suites + proba)
S=1+2+.....+2^n
donc
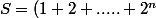(2-1)) (car 2-1=1)
(car 2-1=1)
On développe
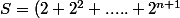-(1+2+......+2^n))
On enlève les ( ) et on simplifie
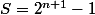
donc
On développe
On enlève les ( ) et on simplifie
Re: DM MATHS 2 exos ( suites + proba)
je l'ai fais a la main
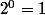
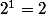
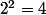
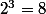
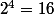
dons pour la somme S si on prend n=3
il faut faire 8 + 4 + 2 + 1=15
et donc pour simplifier on prend l’étape suivante 2^4 qui vaut 16 et on enlève 1
dons pour la somme S si on prend n=3
il faut faire 8 + 4 + 2 + 1=15
et donc pour simplifier on prend l’étape suivante 2^4 qui vaut 16 et on enlève 1
Re: DM MATHS 2 exos ( suites + proba)
la réponse d'aviateur est surement + correcte mais bien moins compréhensible pour un niveau lycée je pense
Re: DM MATHS 2 exos ( suites + proba)
tsunemori a écrit:la réponse d'aviateur est surement + correcte mais bien moins compréhensible pour un niveau lycée je pense
Tu rigoles "développer, simplifier" c'est du niveau collège.
Et puis "l'astuce" multiplier par (2-1) (avec des guillemets bien sûr) ça vient du calcul de la somme des termes d'une suite géométrique. On est à plein tube dans le niveau lycée.
Bon maintenant avec que tu proposes, pour celui qui ne voit pas ou ne sait pas qu'il s'agit de calculer la somme des termes du suite géométrique (et je fais remarquer que le posteur l'avait dit, donc c'est bien comme cela que c'est suggéré de faire), alors on devine avec des exemples la réponse mais une démonstration par récurrence sera à faire malgré tout.
Modifié en dernier par aviateur le 27 Déc 2018, 20:15, modifié 3 fois.
Re: DM MATHS 2 exos ( suites + proba)
on te demande de simplifier la somme infini S en fonction de n
au lieu de devoir écrire chaque terme il faut trouver une formule qui fonctionne pour toutes les valeur de n
donc si tu cherches la somme pour n=3
tu dois additionner tous les terme précédent, donc
au lieu de faire ça tu fais 2^n+1 (dans l'exemple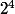 et tu soustrait 1
et tu soustrait 1
au lieu de devoir écrire chaque terme il faut trouver une formule qui fonctionne pour toutes les valeur de n
donc si tu cherches la somme pour n=3
tu dois additionner tous les terme précédent, donc
au lieu de faire ça tu fais 2^n+1 (dans l'exemple
30 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

