DM de maths 1 ère S

[yannp13]

Bonjour je bloque à la première étape de mon DM, j'ai presque tout fait sauf démontrer quelque chose.
Comme je trouve pas comment mettre de photo je vais écrire le sujet : ABCD carré de côté a, M est un point quelconque de (BD), R est le projeté orthogonal de M sur (AB), S est le projeté de M sur (AD).
Démontrez que la droite d1 passant par M et perpendiculaire à (RS) passe par un point fixe.
Voilà il faudrait juste que j'arrive à démontrer pourquoi MR = BR

(Pour info je me suis placé dans le repère (A; AB, AD) puis j'ai calculé un vecteur directeur de (RS) et un vecteur directeur de MC [ici j'ai besoin d'exprimer xM et fonction de yM donc avec MR = BR] puis j'ai fait xx'-yy' et c'est bien = 0)

[mathelot]

Voilà il faudrait juste que j'arrive à démontrer pourquoi MR = BR

Le triangle MBR est rectangle en R. l'angle vaut 45 degrés
car les angles et sont correspondants.

MBR est donc isocèle en R

[yannp13]

D'accord merci beaucoup c'est le truc qui me manquait la correspondance

[yannp13]

Au final je suis bloqué... J'ai cherché environ 4 heures mes erreurs et modifié de nombreuses fois mais je n'arrive toujours pas au bon résultat, je vais dire mes étapes et ça m'aiderait si quelqu'un trouvait où ça plante avec cette méthode.

Repère (A; AB, AD) donc C (1;1), M (1 + m; m), R (1+m; 0) et S (0; m) (m est donc l'ordonnée de M et j'ai exprimé l'abscisse en fonction de l'ordonnée)

Coefficient directeur de (RS) : - m / (1+m)

Donc (RS) : y = (- m / (1+m) ) x + m (car avec S : p = m)

On a donc (- m / (1+m) ) x - y + m = 0

Un vecteur directeur est u (1; -m / (1+m) ) donc un vecteur normal est v (1; -m / (1+m) ) d'où la droite à pour équation : x - m / (1+m) + c = 0

Avec M : c = - (2m + 1) / (1+m)

Donc (d1) : x - (m / (1+m) ) y - (2m + 1) / (1+m) = 0

On vérifie si C respecte l'équation (car C est le point fixe [l'exercice s'appelle recherche de point fixe] d'après GéoGebra) :
[On remplace par 1]

Et j'arrive au résultat 2m / (1+m) qui n'est pas égal à 0 ce qui me pose problème

Merci si quelqu'un vient à lire ceci et à trouver ce qui coince ce serait super j'y suis depuis des heures

[Pisigma]

Bonjour, je pense que tu as oublié ceci:

Si l'équation cartésienne d'une droite (D) est ax+by+c=0, alors un vecteur directeur de (D) est le vecteur de coordonnées (-b,a); un vecteur normal de (D) est le vecteur de coordonnées (a,b)

[yannp13]

Non j'y pensais seulement j'utilise une méthode un peu étrange (à confirmer si on arrive à la même équation) :

Je donne un vecteur v (-b; a) puis je reprends le même vecteur sans changer les coordonnées sauf que ce sera un u (a;b)
Exemple 5x + 2y = 0 v (-2; 5) donc u (-2; 5) et l'autre équation sera -2x + 5y + c = 0

[yannp13]

Ça doit faire une dizaine d'heure et je trouve vraiment pas mon erreur personne pour jeter un oeil ?

[aviateur]

Bonjour
Dès le départ c'est faux. Les coordonnées de M ne sont pas correctes.

[yannp13]

Je ne vois malheureusement pas l'erreur
L'abscisse est 1 + m (ou AB + BR et AB = 1 et BR = RM = m)
Et on nomme l'ordonnée m

[mathelot]

Repère (A; AB, AD) donc C (1;1), M (1 + m; m), R (1+m; 0) et S (0; m)

Bonjour,

M(m;1-m) situé sur la droite (BD) d'équation x+y=1
R(m;0) , S(0;1-m)



vecteur est un vecteur directeur de (d1)



m(-x-y+2)+y-1=0

(d1) passe par le point fixe vérifiant
y=1 et x+y=2 , soit C(1;1)

PS; le tableau carré est le déterminant des vecteurs

[yannp13]

Bonjour, j'ai cherché à modifier tout en m'appuyant sur votre aide mais je ne parviens toujours pas car je n'ai pas la connaissance de ce tableau carré... Je ne sais pas non plus d'où vient ce point N
Je commence à perdre patience tout le monde m'aide et je n'y arrive toujours pas...

[yannp13]

J'ai essayé mais je n'ai pas réussi de passer du vecteur u1 à une nouvelle équation de droite, qui est donc (m - 1) x - m b + c = 0
J'ai cherché la valeur de c avec les coordonnées de m et je trouve -2m^2 + 2m (ce qui me paraît très étrange)
Et quand je finis par tester en remplaçant avec les coordonnées de C, ce qui est donc sensé me donner 0, cela me donne -2m^2 + 2m - 1
Je m'excuse d'avoir autant de mal d'habitude les DM se passent bien mieux que ça...

[aviateur]

Bonjour
Je vais pas tout relire. On peut reprendre, peux tu reprendre en direct car dans 1/2 h j'arrête.
M=(m,1-m) (l'erreur initiale OK?)
R a pour coordonnées et donc
OK?
Ensuite tu cherches une équation de la droite qu'on appelle
qui passe par M et qui est orthogonale à
Soit c'est équivalent à dire
que (produit scalaire tu connais?)
Si oui alors calcules et puis le produit scalaire et tu auras l'équation
de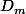 en fonction de m.
J'attends donc l'équation de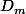
Ensuite pour finir on verra c'est très court.

[yannp13]

Ok c'est plus complexe que ce que je pensais, oui j'ai vu le produit scalaire mais je ne sais pas si j'ai déjà créé un point afin d'en avoir un
Merci je refais ça et je te dis dans 10 20 minutes

[aviateur]

Ok

[yannp13]

Enfin merci beaucoup qu'est ce que j'aurais galéré
J'ai bien calculé le vecteur puis utilisé la propriété que xx' - tu = 0
J'en arrive à l'équation -m x + (1 - m) y + 2m - 1 = 0
Et enfin quand je remplace par les coordonnées de C je tombe bien sur 0
Encore merci et une petite dernière question, comme tu l'as sûrement remarqué je suis nouveau sur le forum alors comment fais tu pour intégrer des flèches de vecteur ou autre à tes messages ?

[aviateur]

\vec{RS} entre 2 balises tex

[yannp13]

J'ai pas du tout compris ton dernier message

[yannp13]

Je suis bête c'est les raccourcis pff je suis ailleurs moi je connais pas les balises tex c'est pour ça

[aviateur]

les balises tex tu les as en utilisant l'éditeur complet