DM Maths 1°S : Barycentres

[juju_11]

[FONT=Comic Sans MS] Bonjour,

J'ai un DM sur les barycentres à faire, et je ne vois pas comment faire.

Voici l'exercice sur lequel je bloque.

ABC est un triangle, G son centre de gravité et K le barycentre des points (A,2), (B,2) et (C,-1).
Déterminer puis construire l'ensemble des points M du plan tels que :
a- E1 : (vecteurs) 2MA + 2 MB - MC soit colinéaire (au vecteur) AB
b- E2 : (norme de vecteurs) [[ 2MA + 2MB - MC ]] = 12
c- E3 : (norme de vecteurs) [[ 2MA + 2MB - MC ]] = [[ MA + MB + MC ]]

Merci d'avance [/FONT]

[Ericovitchi]

Transformes 2MA + 2 MB - MC en utilisant le point K
(et en utilisant la définition du barycentre 2KA+2KB-KC=0)

[ma_y_liss]

bonjours à tous, donc moi aussi j'ai un DM de maths sur les barycentres, j'ai réussi à peu prés tous les exercices sauf un qui me pose probléme, je bloque complètement donc si vous pouviez m'aidez, me guider:
Voila l'ennoncer:

On considère quatre points A,B,C et D du plan.
Déterminer et construire l'ensemble des points M du plan tels que:
||MA+MB+MC||=||4MC-MD|| (ce sont des vecteurs ;))
c'est les seules informations que j'ai...

[benekire2]

bonjours à tous, donc moi aussi j'ai un DM de maths sur les barycentres, j'ai réussi à peu prés tous les exercices sauf un qui me pose probléme, je bloque complètement donc si vous pouviez m'aidez, me guider:
Voila l'ennoncer:

On considère quatre points A,B,C et D du plan.
Déterminer et construire l'ensemble des points M du plan tels que:
||MA+MB+MC||=||4MC-MD|| (ce sont des vecteurs )
c'est les seules informations que j'ai...

Tu ne sais pas comment créer un topic ??
Je t'ai répondu sur le premier ...

[juju_11]

Transformes 2MA + 2 MB - MC en utilisant le point K
(et en utilisant la définition du barycentre 2KA+2KB-KC=0)

Je trouve donc 3MK, ce qui doit être colinéaire à AB.
Comment prouver cette colinéarité ???

Merci.

[benekire2]

Je trouve donc 3MK, ce qui doit être colinéaire à AB.
Comment prouver cette colinéarité ???

Merci.

tu viens de le faire ... MK=1/3 AB donc de la forme MK=kAB donc colinéaires donc tu en déduis M sur la parralèle a AB passant par K

[juju_11]

Ok, merci.

Et pour prouver b- et c- ?? Vous avez un moyen ??
Désolé mais la je bloque, j'ai été absent durant la leçon. :help:

Encore merci de votre aide.

[Dinozzo13]

Salut !
Pour commencer, on remarque que pour les trois cas a-, b- et c-, on a la somme vectorielle or d'après l'énoncé, on a K barycentre de , et donc on peut réduire la somme vectoriel vue précédement en comme tu l'as fait précédement, ce qui nous servira sûrement, ce n'est pas une coincidence si K est défini ainsi sinon il n'aurait pas lieu d'être.

b- L'idée ici est de simplifié la somme vectorielle. Une fois cela fait, on aura une longueur qui est égale à une valeur, l'ensemble cherché sera donc un cercle dont on déterminera le centre et le rayon.

Pour commencer, est le barycentre de , et , donc d'après la propriété fondamentale, pour tout point du plan :
, comme tu l'as fait précédement.
Après tu remplaces ce que tu trouve
équivaut à , tu simplifies cette égalité puis, tu en déduis la nature de l'ensemble cherché et les caractéristiques principales de cet ensemble (bon, biensûr on l'a vu, c'est un cercle, donc il faudra préciser ses caractéristiques, c'est-à-dire son centre et son rayon)

c- Ici, tu as une égalité de normes, l'idée est de simplifier les deux normes. On aura donc, une égalité de longueur donc l'ensemble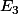 recherché sera ... .
Là encore, on a , or on l'a simplifié précédement donc c'est immédiat.
Ensuite il faut simplifier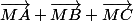 , or d'après l'énoncé, une information importante nous permet de simplifier cette expression sans passer par la propriété fondamentale ( est centre de gravité de ).
Donc après avoir simplifiéles deux normes, tu dis que :
équivaut à , tu simplifies, tu en déduis donc la nature de 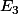ainsi que sa/ses caractéristique(s) principales.

Petite aide pour l'avenir :++:
- Tout ce qui est donné dans l'énoncé est en générale important et donc à utiliser.
- A chaque fois que tu réduis une norme, tu obtiens une longueur qui contient un point quelconque : (en général, on désigne par M le point quelconque).
- Lorsque tu as une égalité de norme de vecteurs, l'ensemble recherché est la médiatrice d'un segment défini par deux points qui ont servis pour réduire les deux normes de vecteurs.
- Lorsque tu as une égalité entre une norme de vecteurs et un réel, il y trois cas possibles :
a) tu as une égalité entre une longueur et un réel strictement positif, l'ensemble recherché est un cercle de centre le point utiliser pour réduire la norme de vecteurs et de rayon égal à la longueur.
b) tu as une longueur qui est égale à 0 alors l'ensemble recherché est un point, et donc les deux points qui définissent cette longueur sont confondus.
c) tu as une égalité entre une longueur et un réel strictement négatif alors l'ensemble est vide, car un cercle ne peut pas avoir un rayon strictement négatif.

Et voilà :++: , en espérant t'avoir aidé.