DM maths 1ère S : Centre du cercle inscrit. Orthocentre. Bar
29 messages
- Page 1 sur 2 - 1, 2
DM maths 1ère S : Centre du cercle inscrit. Orthocentre. Bar
Je suis donc en première S (et depuis cette année je me noie en maths :hum: ) et j'avais un DM à faire pendant les vacances auquel je n'ai strictement rien compris. J'ai fait la question 1. a) et b) mais le reste j'ai abandonné tellement c'est difficile. J'ai demandé de l'aide à mon père qui lui non plus n'a pas compris. J'ai cherché sur d'autres forum mais ça ne m'a pas plus éclairée. Alors je viens vous demander un peu d'aide. Oui c'est vrai, c'est assez long et aussi assez décourageant mais voilà, "I need help" :') ! Merci d'avance pour votre attention.
ABC est un triangle. On note : BC = a, CA = b et AB = c.
L'objectif de ce problème est de trouver des réels x, P, y affectés aux points A, B et C tels que le centre I du cercle inscrit, ou l'orthocentre H de ABC, soit barycentre des sommets.
partie A. Centre du cercle inscrit, point de concours des bissectrices
A' est le pied de la bissectrice de BAC. A' est donc équidistant des côtés de l'angle (propriété caractéristique des points de la bissectrice). On note d cette distance, et h la longueur de la hauteur issue de A.
1. a) Exprimez les aires des triangles AA'B et AA'C de deux façons différentes.
Pour cette question j'ai trouvé : A_AA'B=\frac{(A'B*KA)}{2} et A_AA'B=\frac{(c*d)}{2}
A_AA'C=\frac{(b*d)}{2} et A_AA'C=\frac{(A'C*KA)}{2}
b) Déduisez-en que \frac{A'B}{A'C}=\frac{c}{b}
Pour cela, j'ai utilisé le rapport entre les aires des triangles >
\frac{(A'B*KA)}{2}/\frac{(A'C*KA)}{2}=\frac{A'B}{A'C}
\frac{(c*d)}{2}/\frac{(b*d)}{2}=\frac{c}{b}
Donc \frac{A'B}{A'C}=\frac{c}{b}
2. Prouvez que A' est le barycentre de (B, b) , (C, c) .
J'ai pensé à dire que : B et C sont deux points distincts. La droite (BC) est donc l'ensemble des barycentres de B et C. Or le point A' est situé sur la droite et entre B et C. Nous pouvons en déduire qu'il est alors barycentre de B et C. MAIS, j'ai lu sur un forum que ça ne prouvait pas du tout qu'il était barycentre. Donc après, j'ai pensé utilisé un rapport avec la question 1. b) mais je ne sais pas lequel...
3. B' et C' sont les pieds des bissectrices de ABC et de ACB. Exprimez B' comme barycentre de C et A d'une part, et C' comme barycentre de A et B d'autre part.
4. Démontrez que le point I est le barycentre de (A, a) , (B, b) et (C, c) .
partie B. Orthocentre, point de concours des hauteurs
Pour la démonstration, on se place uniquement dans le cas où les angles de ABC sont tous aigus.
Dans cette partie, je n'ai vraiment rien rien rien compris :mur: . Comment utiliser les barycentres avec les tangentes ? Quel rapport disons ?
1. a) Prouvez que \frac{KB}{KC}=tan \hat{C}
tan B
b) Justifiez que K, pied de la hauteur issue de A, est le barycentre de (B, tan \hat{B}) , (C, tan \hat{C}) .
2. Donnez des résultats analogues pour les pieds L et M des hauteurs issues de B et C.
3. Prouvez par une méthode analogue à celle de la partie A que l'orthocentre est le barycentre de (A, tan \hat{A}), (B, tan \hat{B}) et (C, tan \hat{C}) .
Note : Ce résultat reste valable dans le cas de tout triangle, non rectangle.
ABC est un triangle. On note : BC = a, CA = b et AB = c.
L'objectif de ce problème est de trouver des réels x, P, y affectés aux points A, B et C tels que le centre I du cercle inscrit, ou l'orthocentre H de ABC, soit barycentre des sommets.
partie A. Centre du cercle inscrit, point de concours des bissectrices
A' est le pied de la bissectrice de BAC. A' est donc équidistant des côtés de l'angle (propriété caractéristique des points de la bissectrice). On note d cette distance, et h la longueur de la hauteur issue de A.
1. a) Exprimez les aires des triangles AA'B et AA'C de deux façons différentes.
Pour cette question j'ai trouvé : A_AA'B=\frac{(A'B*KA)}{2} et A_AA'B=\frac{(c*d)}{2}
A_AA'C=\frac{(b*d)}{2} et A_AA'C=\frac{(A'C*KA)}{2}
b) Déduisez-en que \frac{A'B}{A'C}=\frac{c}{b}
Pour cela, j'ai utilisé le rapport entre les aires des triangles >
\frac{(A'B*KA)}{2}/\frac{(A'C*KA)}{2}=\frac{A'B}{A'C}
\frac{(c*d)}{2}/\frac{(b*d)}{2}=\frac{c}{b}
Donc \frac{A'B}{A'C}=\frac{c}{b}
2. Prouvez que A' est le barycentre de (B, b) , (C, c) .
J'ai pensé à dire que : B et C sont deux points distincts. La droite (BC) est donc l'ensemble des barycentres de B et C. Or le point A' est situé sur la droite et entre B et C. Nous pouvons en déduire qu'il est alors barycentre de B et C. MAIS, j'ai lu sur un forum que ça ne prouvait pas du tout qu'il était barycentre. Donc après, j'ai pensé utilisé un rapport avec la question 1. b) mais je ne sais pas lequel...
3. B' et C' sont les pieds des bissectrices de ABC et de ACB. Exprimez B' comme barycentre de C et A d'une part, et C' comme barycentre de A et B d'autre part.
4. Démontrez que le point I est le barycentre de (A, a) , (B, b) et (C, c) .
partie B. Orthocentre, point de concours des hauteurs
Pour la démonstration, on se place uniquement dans le cas où les angles de ABC sont tous aigus.
Dans cette partie, je n'ai vraiment rien rien rien compris :mur: . Comment utiliser les barycentres avec les tangentes ? Quel rapport disons ?
1. a) Prouvez que \frac{KB}{KC}=tan \hat{C}
tan B
b) Justifiez que K, pied de la hauteur issue de A, est le barycentre de (B, tan \hat{B}) , (C, tan \hat{C}) .
2. Donnez des résultats analogues pour les pieds L et M des hauteurs issues de B et C.
3. Prouvez par une méthode analogue à celle de la partie A que l'orthocentre est le barycentre de (A, tan \hat{A}), (B, tan \hat{B}) et (C, tan \hat{C}) .
Note : Ce résultat reste valable dans le cas de tout triangle, non rectangle.
Hello,
Bon je me dévoue pour venir t'aider ^^ bien que ce soit un peu difficile à lire vu que tu as zappé les balises TEX
On a bien l'aire de AA'B qui vaut en utilisant la formule aire = base*hauteur/2 et l'aire de AA'C qui vaut
en utilisant la formule aire = base*hauteur/2 et l'aire de AA'C qui vaut  .
.
En introduisant la hauteur issue de A dont on note la longueur h, on a aussi l'aire de AA'B qui vaut \frac{A'B.h}{2} et l'aire de AA'C qui vaut \frac{A'C.h}{2}
Ce qui permet de dire que et donc
et donc  .
.
Cette expression te donne par produit en croix b.A'B = c.A'C
Or comme B,A' et C sont alignés, ceci se traduit soit par soit par
soit par  ...
...
Tu devrais maintenant pouvoir conclure quant à la question 2 ...
Bon je me dévoue pour venir t'aider ^^ bien que ce soit un peu difficile à lire vu que tu as zappé les balises TEX
On a bien l'aire de AA'B qui vaut
En introduisant la hauteur issue de A dont on note la longueur h, on a aussi l'aire de AA'B qui vaut \frac{A'B.h}{2} et l'aire de AA'C qui vaut \frac{A'C.h}{2}
Ce qui permet de dire que
Cette expression te donne par produit en croix b.A'B = c.A'C
Or comme B,A' et C sont alignés, ceci se traduit soit par
Tu devrais maintenant pouvoir conclure quant à la question 2 ...
Je reposte une seconde fois avec les balises TEX... Désolée.
ABC est un triangle. On note : BC = a, CA = b et AB = c.
L'objectif de ce problème est de trouver des réels x, P, y affectés aux points A, B et C tels que le centre I du cercle inscrit, ou l'orthocentre H de ABC, soit barycentre des sommets.
partie A. Centre du cercle inscrit, point de concours des bissectrices
A' est le pied de la bissectrice de BAC. A' est donc équidistant des côtés de l'angle (propriété caractéristique des points de la bissectrice). On note d cette distance, et h la longueur de la hauteur issue de A.
1. a) Exprimez les aires des triangles AA'B et AA'C de deux façons différentes.
Pour cette question j'ai trouvé : A_AA'B=}{2}) et A_AA'B=
et A_AA'B=}{2})
A_AA'C=}{2}) et A_AA'C=
et A_AA'C=}{2}) b) Déduisez-en que
b) Déduisez-en que  =
=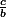
Pour cela, j'ai utilisé le rapport entre les aires des triangles >
}{2}) /
/}{2}) =
=
}{2}) /
/}{2}) =
=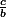
Donc =
=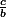
2. Prouvez que A' est le barycentre de (B, b) , (C, c) .
J'ai pensé à dire que : B et C sont deux points distincts. La droite (BC) est donc l'ensemble des barycentres de B et C. Or le point A' est situé sur la droite et entre B et C. Nous pouvons en déduire qu'il est alors barycentre de B et C. MAIS, j'ai lu sur un forum que ça ne prouvait pas du tout qu'il était barycentre. Donc après, j'ai pensé utilisé un rapport avec la question 1. b) mais je ne sais pas lequel...
3. B' et C' sont les pieds des bissectrices de ABC et de ACB. Exprimez B' comme barycentre de C et A d'une part, et C' comme barycentre de A et B d'autre part.
4. Démontrez que le point I est le barycentre de (A, a) , (B, b) et (C, c) .
partie B. Orthocentre, point de concours des hauteurs
Pour la démonstration, on se place uniquement dans le cas où les angles de ABC sont tous aigus.
Dans cette partie, je n'ai vraiment rien rien rien compris . Comment utiliser les barycentres avec les tangentes ? Quel rapport disons ?
1. a) Prouvez que =
=
b) Justifiez que K, pied de la hauteur issue de A, est le barycentre de (B, tan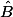 ) , (C, tan
) , (C, tan 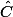 ) .
) .
2. Donnez des résultats analogues pour les pieds L et M des hauteurs issues de B et C.
3. Prouvez par une méthode analogue à celle de la partie A que l'orthocentre est le barycentre de (A, tan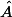 ), (B, tan
), (B, tan 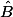 ) et (C, tan
) et (C, tan 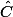 ) .
) .
Note : Ce résultat reste valable dans le cas de tout triangle, non rectangle.
ABC est un triangle. On note : BC = a, CA = b et AB = c.
L'objectif de ce problème est de trouver des réels x, P, y affectés aux points A, B et C tels que le centre I du cercle inscrit, ou l'orthocentre H de ABC, soit barycentre des sommets.
partie A. Centre du cercle inscrit, point de concours des bissectrices
A' est le pied de la bissectrice de BAC. A' est donc équidistant des côtés de l'angle (propriété caractéristique des points de la bissectrice). On note d cette distance, et h la longueur de la hauteur issue de A.
1. a) Exprimez les aires des triangles AA'B et AA'C de deux façons différentes.
Pour cette question j'ai trouvé : A_AA'B=
A_AA'C=
Pour cela, j'ai utilisé le rapport entre les aires des triangles >
Donc
2. Prouvez que A' est le barycentre de (B, b) , (C, c) .
J'ai pensé à dire que : B et C sont deux points distincts. La droite (BC) est donc l'ensemble des barycentres de B et C. Or le point A' est situé sur la droite et entre B et C. Nous pouvons en déduire qu'il est alors barycentre de B et C. MAIS, j'ai lu sur un forum que ça ne prouvait pas du tout qu'il était barycentre. Donc après, j'ai pensé utilisé un rapport avec la question 1. b) mais je ne sais pas lequel...
3. B' et C' sont les pieds des bissectrices de ABC et de ACB. Exprimez B' comme barycentre de C et A d'une part, et C' comme barycentre de A et B d'autre part.
4. Démontrez que le point I est le barycentre de (A, a) , (B, b) et (C, c) .
partie B. Orthocentre, point de concours des hauteurs
Pour la démonstration, on se place uniquement dans le cas où les angles de ABC sont tous aigus.
Dans cette partie, je n'ai vraiment rien rien rien compris . Comment utiliser les barycentres avec les tangentes ? Quel rapport disons ?
1. a) Prouvez que
b) Justifiez que K, pied de la hauteur issue de A, est le barycentre de (B, tan
2. Donnez des résultats analogues pour les pieds L et M des hauteurs issues de B et C.
3. Prouvez par une méthode analogue à celle de la partie A que l'orthocentre est le barycentre de (A, tan
Note : Ce résultat reste valable dans le cas de tout triangle, non rectangle.
La question 1 te donne une relation sur les longueurs.
Pour répondre à la question 2 il faut une relation sur les vecteurs.
Contrairement à la relation sur les vecteurs, la relation sur les longueurs n'a pas la notion de sens (qui se traduit par un signe + ou -).
C'est pourquoi b.A'B = c.A'C peut se traduire par ou bien par
ou bien par  ... il faut voir quelle relation correspond au cas étudié.
... il faut voir quelle relation correspond au cas étudié.
Pour répondre à la question 2 il faut une relation sur les vecteurs.
Contrairement à la relation sur les vecteurs, la relation sur les longueurs n'a pas la notion de sens (qui se traduit par un signe + ou -).
C'est pourquoi b.A'B = c.A'C peut se traduire par
C'est tout ? Bon, en fait ce n'était pas si compliqué après tout...
Pour la question 3. j'ai trouvé cela, même si je ne pense pas qu'il faille juste l'exprimer comme cela :
B' étant le pied de la bissectrice de l'angle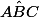 il se trouve alors sur le côté opposé à cet angle qui est [AC]. Il est donc barycentre de C et A : y
il se trouve alors sur le côté opposé à cet angle qui est [AC]. Il est donc barycentre de C et A : y =-x
=-x > y
> y +x
+x =
=
C' étant le pied de la bissectrice de l'angle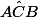 il se trouve alors sur le côté opposé à cet angle qui est [AB]. Il est donc barycentre de A et B : x
il se trouve alors sur le côté opposé à cet angle qui est [AB]. Il est donc barycentre de A et B : x =-P
=-P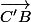 > x
> x +P
+P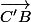 =
=
Pour la question 3. j'ai trouvé cela, même si je ne pense pas qu'il faille juste l'exprimer comme cela :
B' étant le pied de la bissectrice de l'angle
C' étant le pied de la bissectrice de l'angle
DM maths 1ère S : Centre du cercle inscrit. Orthocentre. Barycentres
Bonjour , je suis bloqué au même niveau que Solene , et je ne vois aucun rapport :/
29 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
