Mathématiques seconde

[Ben314]

Je ne sait que répondre à de si subtils et profonds arguments.... (*)

Et....

Soit l'unique racine réelle du polynôme .
Question 1) Montrer que .... (a toi de continuer)
Indication : on pourra utiliser les formules de Cardan

J'attend toujours...

P.S. (*) Ah, si, j'ai bien une idée : "c'est celui qui dit..."
mais bon, j'ai un peu passé l'âge pour ce genre de réplique (ainsi que pour écrire des commentaires du type du tien...)

[Black Jack]

Tu peux attendre tant que tu veux.

A partir du moment où la racine est trouvée (Ici par Cardan ou autrement) en moins de temps qu'il ne faut pour le dire. (ce ne serait pas pareil autrement que par Ferrari pour une équation du quatrième degré à coefficients réels avec 4 racines complexes et bien entendu sans confier les calculs à une calculette prévue pour).

On peut poser la question qu'on veut à propos de cette racine, on a aussi la réponse immédiatement.

C'est tellement évident que c'est pitoyable d'insister sur cette "non difficulté".

Mais c'est peut être difficile à comprendre pour certains.

Maintenant, si la question était aussi sotte que "Montrer que xo n'est pas égal à 0" ou une autre biscornuterie du même acabit, on n'aurait nul besoin de Cardan.

Je termine ici sur le sujet, il n'y a de pire sourd que celui qui ne veut pas entendre ... et ne réchigne pas à nier l'évidence.

[Ben314]

Tu peux attendre tant que tu veux.

Donc c'est super archi vachement utile (donc trivial de donner un exemple de la fameuse utilité), tu t'énerve de plus en plus MAIS tu refuse de me donner ce fameux exemple que j'attends (patiemment).
Tu ne trouve pas ça un peu... étrange... on va dire ?

On peut poser la question qu'on veut à propos de cette racine, on a aussi la réponse immédiatement.

Totalement faux (10em édition). Même la question la plus simple qui soit, c'est à dire "est ce que c'est égal à 1" tu ne peut pas y répondre.

Maintenant, si la question était aussi sotte que "Montrer que xo n'est pas égal à 0" ou une autre biscornuterie du même acabit, on n'aurait nul besoin de Cardan.

Là, O.K. et je pense qu'effectivement il n'y a absolument rien a rajouter.
Si pour toi " On peut répondre à toute les questions concernant x, sauf les questions sottes et biscornues comme par exemple de savoir s'il est égal à 1 ou pas", je n'insisterais effectivement pas une seconde de plus vu que j'ai une opinion bien différente de ce qui est une "question sotte et biscornue".

Par contre, juste par curiosité, vu que, quand on a un réel x, c'est des questions "sottes et biscornues" de se demander s'il est égal à 1, plus grand que 3, plus petit que 7, si c'est un entier, un rationnel (enfin toute les question auquel tu ne peut pas répondre avec la forme de Cardan), ça serait quoi une "question intelligente" ?

P.S. Et j'ai un peu beaucoup passé l'age des insultes et autre insinuations vaseuses, donc si tu pouvait t'abstenir et t'en tenir à un discours rationnel et argumenté, j'apprécierais fortement.
Merci par avance.

[Black Jack]

Comment être aussi borné ?

Si on veut savoir si xo = 1 convient, on calcule f(1) est on a la réponse directement.

Cela fait partie des biscornuterie mentionnées.

Pareil pour xo > 3 ou xo < 7 avec une équation aussi simple que x³+x+1 = 0 où il est évident au premier regard, sans calculs que f est croissante partout.

Cela fait partie des biscornuteries...

Tu peux nier tant que tu veux, l'intérêt de Cardan ou Ferrari, c'est un non sens.

Ceci ne signifie en rien qu'on ne puisse pas réfléchir, sur des questions concrètes, autrement qu'en utilisant Cardan ou Ferrari...
Je n'ai jamais dit, ni pensé cela.
Je l'ai d'ailleurs clairement fait comprendre dès ma réponse d'origine dans laquelle, ayant mal lu la question, j'ai clairement écrit ne pas y avoir répondu par Cardan.

Par contre, je pense toujours qu'un outil (Cardan ou Ferrari) qui permet de résoudre certains types d'équation parfois pas très faciles (4eme degré non bicarrée à coeff réels et solutions unuiquement complexes par exemple) à résoudre par d'autres méthodes ne peut pas être sottement repoussé d'un revers de la main.

L'argument, qu'on peut confier cela à une "calculette prévue pour" et que donc c'est inutile est aussi *** que le message d'un certain politique qui avait annoncé "qu'on pouvait virer des programmes l'étude des fonctions parce que, de toutes manières, les calculettes graphiques faisaient cela plus vite et mieux que les étudiants.

J'en reste là définitivement sur ce sujet.

[Ben314]

Comment être aussi borné ?
Tu peux nier tant que tu veux, l'intérêt de Cardan ou Ferrari, c'est un non sens.
...ne peut pas être sottement repoussé d'un revers de la main.

Est ce que, s'il te plait, tu pourrait te comporter comme un adulte et éviter ce type de commentaire sans le moindre intérêt pour te concentrer sur des argument rationnels.
Par avance, merçi (2em édition...)

Par contre, je pense toujours qu'un outil (Cardan ou Ferrari) qui permet de résoudre certains types d'équation parfois pas très faciles

Le fond du problème, il est très exactement là.
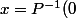Personnellement, et je pense être loin d'être le seul, le fait de "résoudre", une équation, ça ne signifie pas seulement écrire x=quelque_chose, par exemple (et j'en ait déjà parlé), si on écrit uniquement , je ne considère pas qu'on a "résolu" quoi que ce soit.
Pour qu'on ait effectivement "résolu" l'équation, il faut que le "quelque chose" à droite du = apporte de l'information, sinon on n'a rien résolu du tout. Et comme, les formules de Cardan ne permettent de répondre à aucune question concernant le x, ben... elles n'apportent rien.

L'argument, qu'on peut confier cela à une "calculette prévue pour" et que donc c'est inutile est aussi *** que le message d'un certain politique qui avait annoncé "qu'on pouvait virer des programmes l'étude des fonctions parce que, de toutes manières, les calculettes graphiques faisaient cela plus vite et mieux que les étudiants.

A part d'enfoncer le clou dans le style "je m'énerve de plus en plus jusqu'à me comporter comme un gamin de 5 ans et je raconte n'importe quoi", je comprend pas bien l'essence de cette remarque.
Tu pourrais un peu développer concernant le lien que tu fait entre les formules de Cardan et l'étude des fonctions ?
Parce que je te rappelle, que, pas plus qu'aux autres question, tu n'a répondu à celle posé concernant l'utilité "formelle" des fameuses formules et que pour le moment, tout ce que tu as dit concernant ce qu'on pouvait faire avec, c'était de les rentrer dans une calculette pour avoir une valeur approchée. Et qu'effectivement, je t'ai rétorqué que, si c'est pour finir par sortir la calculette, autant la sortir dés le début, ça va bien plus vite et c'est au moins aussi précis. Enfin, bref, je vois pas le début de la moitié du rapport que ça pourrait avoir avec le fait de savoir faire une étude de fonction sans calculette du début à la fin.