Mathématiques seconde
25 messages
- Page 1 sur 2 - 1, 2
mathématiques seconde
Bonjour, je suis nouveau membre sur le site et dois expliquer un devoir à mon fils en seconde qui est souffrant.
Montrer que l'équation x (au cube) - racine carré de 2x +2=O n'a pas de solution qui soit un nombre rationnel.
Je vous remercie d'avance.
Montrer que l'équation x (au cube) - racine carré de 2x +2=O n'a pas de solution qui soit un nombre rationnel.
Je vous remercie d'avance.
Re: mathématiques seconde
Salut,
Moi, je voterais plutôt pour ça .
.
(c'est à quelle heure le dépouillement ?)
Moi, je voterais plutôt pour ça
(c'est à quelle heure le dépouillement ?)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: mathématiques seconde
Cardan.
x³ + px + q = 0
avec p = -V2 et q = 2
On calcule (q/2)² + (p/3)³ et on voit que c'est > 0
On a alors :
1 racine réelle R.
^2+(\frac{p}{3})^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{(\frac{q}{2})^2+(\frac{p}{3})^3}})
Il y a aussi 2 racines complexes conjuguées C1 et C2.
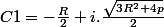
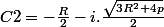
Soit on refait la démo (pour les maso), soit on retient les résultats dans un formulaire.

Edit
Oublier ma réponse (bien qu'elle donne les solutions).
Je n'ai pas répondu à la question posée.
x³ + px + q = 0
avec p = -V2 et q = 2
On calcule (q/2)² + (p/3)³ et on voit que c'est > 0
On a alors :
1 racine réelle R.
Il y a aussi 2 racines complexes conjuguées C1 et C2.
Soit on refait la démo (pour les maso), soit on retient les résultats dans un formulaire.
Edit
Oublier ma réponse (bien qu'elle donne les solutions).
Je n'ai pas répondu à la question posée.
Re: mathématiques seconde
tu peux supposer qu'il y a une racine de la forme a/b (a et b entiers et a/b irréductible) et montrer qu'il y a une impossibilité.
Re: mathématiques seconde
Black Jack a écrit:Cardan.
x³ + px + q = 0
avec p = -V2 et q = 2
On calcule (q/2)² + (p/3)³ et on voit que c'est > 0
On a alors :
1 racine réelle R.
Il y a aussi 2 racines complexes conjuguées C1 et C2.
Soit on refait la démo (pour les maso), soit on retient les résultats dans un formulaire.
Edit
Oublier ma réponse (bien qu'elle donne les solutions).
Je n'ai pas répondu à la question posée.
Je vous remercie mais c'est du chinois pour moi et suis incapable de réexpliquer cette solution.
Re: mathématiques seconde
Je sais pas si c'est du chinois, mais par contre, c'est clairement "un bulldozer pour écraser une mouche".
Sans parler du fait que les formules de Cardan, ça ne risque pas de servir pour savoir si une solution est rationnelle ou pas vu que, même dans le cas où il y une solution entière simple à l'équation, par exemple x=1, les formules de Cardan donnent un truc abominable et que si on veut montrer que le truc abominable vaut en fait 1, ben la seule méthode, c'est de refaire le travail à l'envers pour montrer que le truc abominable vérifie une certaine équation qui a comme racine évidente x=1.
Enfin, bref, dans ce type de contexte comme dans des tonnes d'autres, ça n'a aucun intérêt les formules de Cardan (si on ne les voit qu'en L3/M1 au moment où on voit la théorie de Galois, c'est qu'elles n'ont pas d'intérêt à part comme exemple de la théorie de Galois)
Méthode I : Si alors
alors  est forcément non nul et on a
est forcément non nul et on a  qui, si x était rationnel (non nul) serait lui même rationnel. Or on sait que
qui, si x était rationnel (non nul) serait lui même rationnel. Or on sait que  n'est pas rationnel.
n'est pas rationnel.
Méthode II : Si alors
alors ^2\!=\!(x^3\!+\!2)^2\!=\!x^6\!+\!4x^3\!+\!4) c'est à dire
c'est à dire  .
.
Si une telle équation avait une solution rationnelle (irréductible et avec q>0) on aurait
(irréductible et avec q>0) on aurait ^6\!+\!4(\frac{p}{q})^3\!-\!2\!(\frac{p}{q})^2\!+\!4\!=\!0) et donc (en multipliant par
et donc (en multipliant par  ) :
) :  .
.
- Les trois derniers termes étant des entiers divisible par le premier
le premier  (qui est égal à l'opposé de la somme des 3 derniers) l'est aussi donc
(qui est égal à l'opposé de la somme des 3 derniers) l'est aussi donc  (car p et q sont sans facteurs communs).
(car p et q sont sans facteurs communs).
- Les trois premier termes étant divisible par le quatrième
le quatrième  (qui est égal à l'opposé de la somme des 3 premiers) l'est aussi donc
(qui est égal à l'opposé de la somme des 3 premiers) l'est aussi donc  divise 4 (car p et q sont sans facteurs communs).
divise 4 (car p et q sont sans facteurs communs).
Bilan : Les seuls rationels éventuellement solution de l'équation sont -4, -2, -1, 1, 2, 4 sauf qu'en fait aucun des 6 ne marche.
Sans parler du fait que les formules de Cardan, ça ne risque pas de servir pour savoir si une solution est rationnelle ou pas vu que, même dans le cas où il y une solution entière simple à l'équation, par exemple x=1, les formules de Cardan donnent un truc abominable et que si on veut montrer que le truc abominable vaut en fait 1, ben la seule méthode, c'est de refaire le travail à l'envers pour montrer que le truc abominable vérifie une certaine équation qui a comme racine évidente x=1.
Enfin, bref, dans ce type de contexte comme dans des tonnes d'autres, ça n'a aucun intérêt les formules de Cardan (si on ne les voit qu'en L3/M1 au moment où on voit la théorie de Galois, c'est qu'elles n'ont pas d'intérêt à part comme exemple de la théorie de Galois)
Méthode I : Si
Méthode II : Si
Si une telle équation avait une solution rationnelle
- Les trois derniers termes étant des entiers divisible par
- Les trois premier termes étant divisible par
Bilan : Les seuls rationels éventuellement solution de l'équation sont -4, -2, -1, 1, 2, 4 sauf qu'en fait aucun des 6 ne marche.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: mathématiques seconde
J'ai bien mentionné ne pas avoir répondu à la question ... (que je n'avais pas lue jusqu'au bout)
Par contre la remarque sur Cardan de Ben314 est parfaitement inadéquate ... quand il s'agit de résoudre une équation de ce type sans solutions "évidentes" entières ou rationnelles.
Pas plus qu'on ne redémontre un théorème à chaque utilisation dans une démo, on n'est censé réappliquer toute la méthode de Cardan lors de la résolution de ce type d'équations (3eme degré à coeff réels).
Après avoir vérifié s'il n'existait pas de solutions "évidentes", on ramene l'équation (par un simple changement de variables) sous la forme x³ + px + q = 0
Il suffit de calculer numériquement le "q/2)² + (p/3)³" et suivant le résultats, trouver l'expression des solutions dans un "pense-bête" qu'on n'écrit qu'une seule fois.
La seule petite difficulté (et encore) est lorsque on a 3 solutions réelles où les solutions sont données avec des cosinus.
Mais ce n'était, bien sûr, pas ce qui était demandé dans cet exercice-ci.

Par contre la remarque sur Cardan de Ben314 est parfaitement inadéquate ... quand il s'agit de résoudre une équation de ce type sans solutions "évidentes" entières ou rationnelles.
Pas plus qu'on ne redémontre un théorème à chaque utilisation dans une démo, on n'est censé réappliquer toute la méthode de Cardan lors de la résolution de ce type d'équations (3eme degré à coeff réels).
Après avoir vérifié s'il n'existait pas de solutions "évidentes", on ramene l'équation (par un simple changement de variables) sous la forme x³ + px + q = 0
Il suffit de calculer numériquement le "q/2)² + (p/3)³" et suivant le résultats, trouver l'expression des solutions dans un "pense-bête" qu'on n'écrit qu'une seule fois.
La seule petite difficulté (et encore) est lorsque on a 3 solutions réelles où les solutions sont données avec des cosinus.
Mais ce n'était, bien sûr, pas ce qui était demandé dans cet exercice-ci.
Re: mathématiques seconde
- Au niveau "à la main", c'est sans le moindre intérêt : tu va avoir des racines cubiques de trucs contenant des racines carrées dont te ne pourra absolument pas savoir si ça se simplifie ou pas (sauf en revenant en arrière pour remonter à l'équation de base). Par exemple, si tu exprime les solution d'une équation du 3em degrés avec Cardan puis qu'on te demande si x=3 est ou pas une solution de l'équation, ben c'est pas en regardant tes fameuses "solutions" que tu le saura (il me semble quand même que ça prouve on ne peut mieux l'inutilité du bidule, non ?)
- Au niveau calcul avec machine, c'est quasi sans intérêt (*) vu que de toute façon, le calcul des racines cubiques (éventuellement complexes), la machine va les faire via des processus itératif d'approximation donc aussi bien, tu peut des le départ chercher les solutions de l'équation par des processus itératifs. Et de procéder de cette façon là, ça a l'énorme avantage que tu va pas être bloqué au niveau du degrés 5 du fait qu'on ne peut plus exprimer les solutions à l'aide de radicaux.
(*) Le seul intérêt, au niveau machine, il est pas théorique, mais pratique : la fonction racine cubique (réelle) est souvent déjà implémenté sur la machine et d'implémenter une fonction racine cubique complexe, si elle existe pas, c'est pas sorcier. Et évidement en terme de temps passé à taper du code, ça va plus vite d'utiliser des trucs déjà implémentés.
Par contre, au niveau vitesse de calcul et/ou précision des calculs, tu y perd plus que tu y gagne (par rapport à une implémentation "directe" ou tu cherche directement des approximations des solutions de l'équation).
Bref, je persiste et je signe : a part de très rares cas particuliers, ça sert absolument à rien les formules de Cardan (et de Ferrari) et ça se voit en particulier très bien dans un exo tel que celui là où en les écrivant, non seulement tu n'avance pas vers la solution de l'exo., mais même tu recule vu que, partant de ton x=racine_cubique(...), si on te demande si x est rationnel ou pas, il faut commencer par retrouver l'équation du 3em degré d'où provient x.
Pour poser le problème différemment, peut tu peut me donner ne serait-ce qu'un exemple d'exercice avec un polynôme du 3em degré (qu'on va supposer pour simplifier admettre une unique racines réelle) où on te pose une question concernant la racine (est-elle plus grande que 3 ? , appartient-elle à tel ensemble ? a-t-elle cette propriété ?, etc etc) et où l'expression de la racine avec les formule de Cardan puisse servir à quoi que ce soit ?
- Au niveau calcul avec machine, c'est quasi sans intérêt (*) vu que de toute façon, le calcul des racines cubiques (éventuellement complexes), la machine va les faire via des processus itératif d'approximation donc aussi bien, tu peut des le départ chercher les solutions de l'équation par des processus itératifs. Et de procéder de cette façon là, ça a l'énorme avantage que tu va pas être bloqué au niveau du degrés 5 du fait qu'on ne peut plus exprimer les solutions à l'aide de radicaux.
(*) Le seul intérêt, au niveau machine, il est pas théorique, mais pratique : la fonction racine cubique (réelle) est souvent déjà implémenté sur la machine et d'implémenter une fonction racine cubique complexe, si elle existe pas, c'est pas sorcier. Et évidement en terme de temps passé à taper du code, ça va plus vite d'utiliser des trucs déjà implémentés.
Par contre, au niveau vitesse de calcul et/ou précision des calculs, tu y perd plus que tu y gagne (par rapport à une implémentation "directe" ou tu cherche directement des approximations des solutions de l'équation).
Bref, je persiste et je signe : a part de très rares cas particuliers, ça sert absolument à rien les formules de Cardan (et de Ferrari) et ça se voit en particulier très bien dans un exo tel que celui là où en les écrivant, non seulement tu n'avance pas vers la solution de l'exo., mais même tu recule vu que, partant de ton x=racine_cubique(...), si on te demande si x est rationnel ou pas, il faut commencer par retrouver l'équation du 3em degré d'où provient x.
Pour poser le problème différemment, peut tu peut me donner ne serait-ce qu'un exemple d'exercice avec un polynôme du 3em degré (qu'on va supposer pour simplifier admettre une unique racines réelle) où on te pose une question concernant la racine (est-elle plus grande que 3 ? , appartient-elle à tel ensemble ? a-t-elle cette propriété ?, etc etc) et où l'expression de la racine avec les formule de Cardan puisse servir à quoi que ce soit ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: mathématiques seconde
Eh ben si c'est inepte, ça doit vouloir dire que, face à ça :
Donc... j'attends patiemment ta réponse... (et je reprécise que je te laisse parfaitement libre de la question qu'on pose concernant la racine du polynôme)
Tu ne doit avoir que l'embarra du choix.Ben314 a écrit:Peut tu peut me donner ne serait-ce qu'un exemple d'exercice avec un polynôme du 3em degré (qu'on va supposer pour simplifier admettre une unique racines réelle) où on te pose une question concernant la racine (est-elle plus grande que 3 ? , appartient-elle à tel ensemble ? a-t-elle cette propriété ?, etc etc) et où l'expression de la racine avec les formule de Cardan puisse servir à quoi que ce soit ?
Donc... j'attends patiemment ta réponse... (et je reprécise que je te laisse parfaitement libre de la question qu'on pose concernant la racine du polynôme)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: mathématiques seconde
Pas besoin d'exemples particuliers.
Annoncer qu'une méthode qui permet de trouver les racines exactes de toute équation à coefficients réels du 3ème degré (Cardan) ou du 4ème degré (Ferrari) est tout simplement idiot.
Certes, dans la plupart des applications, on peut se contenter de valeurs approchées des solutions, mais cela n'enlève en rien l'utilité de les connaître exactement ou du moins de les avoir sous forme de "relations" comme celles de mon premier message.
Ne serait-ce (et même si on en perd au final la valeur exacte en cours de calculs) que pour utiliser ces "formules de Cardan" pour en manipuler les résultats dans des algos dans les programmes d'informatique.
Et pourquoi s'arrêter aux seules solution réelles ?
Pour Ferrari (4 ème degré), il pourrait bien ne pas avoir de telles solutions.
Nier l'intérêt de Cardan ou Ferrari est dans la même lignée que de nier l'intérêt des méthodes largement utilisées et connues pour trouver les solutions du équation du 2ème degré.
Penses-en ce que tu veux, c'est simplement idiot.

Annoncer qu'une méthode qui permet de trouver les racines exactes de toute équation à coefficients réels du 3ème degré (Cardan) ou du 4ème degré (Ferrari) est tout simplement idiot.
Certes, dans la plupart des applications, on peut se contenter de valeurs approchées des solutions, mais cela n'enlève en rien l'utilité de les connaître exactement ou du moins de les avoir sous forme de "relations" comme celles de mon premier message.
Ne serait-ce (et même si on en perd au final la valeur exacte en cours de calculs) que pour utiliser ces "formules de Cardan" pour en manipuler les résultats dans des algos dans les programmes d'informatique.
Et pourquoi s'arrêter aux seules solution réelles ?
Pour Ferrari (4 ème degré), il pourrait bien ne pas avoir de telles solutions.
Nier l'intérêt de Cardan ou Ferrari est dans la même lignée que de nier l'intérêt des méthodes largement utilisées et connues pour trouver les solutions du équation du 2ème degré.
Penses-en ce que tu veux, c'est simplement idiot.
Re: mathématiques seconde
Personnellement, je trouve ça "à peine gonflé" de prétendre que lorsque l'on écrit x=racine_cubique(...)+racine_cubique(...), celà permet de "connaitre exactement x" (c'est ce que tu as écrit) sachant qu'en fait cette écriture ne permet même pas de répondre à la malheureuse question "est-ce que x=1 ?"
(contrairement à l'écriture des solution d'une équation du second degré)
Pour faire un peu d'humour, vu que toi, lorsque tu "connait exactement un réel x", ça signifie qu'en fait tu ne sait même pas s'il est égal à 1 (ni s'il est plus grand ou plus petit que 1 d'ailleurs), je me demande ce que ça doit être lorsque tu "ne le connais pas exactement"....
Et, sinon, par exemple (et... par hasard...) il me semble que c'est justement le fait que cette écriture à, on va dire poliment "le mauvais gout" de ne même pas permettre de répondre à la question "est-ce que x=1" qu'il est clair que ça n'a absolument aucun intérêt de la "manipuler" comme tu dit dans un quelconque logiciel de calcul formel (ou encore pire à la main). On aura comme résultat de la "manipulation" un truc du même genre, c'est à dire dont on est complètement incapable de savoir s'il est égal (ou pas) à une autre expression, même si la deuxième expression est aussi simple que "1".
Le premier exemple qui me vient à l'esprit, c'est celui de l'andouille qui, pour savoir si le x en question est racine ou pas d'un second polynôme Q, va "injecter" la formule de cardan dans le second polynôme. Il aura certes une zolie expression finale (d'éventuellement 3 pages...), mais qui aura de nouveau le "mauvais gout" qu'il n'y aura aucun moyen de savoir si l'expression trouvée vaut 0 ou pas (à part évidement en refaisant tout les calculs à l'envers pour remonter aux deux polynômes de départ). Donc de nouveau un truc abominable qui aura pas permis d'avancer d'un millimètre en ce qui concerne la question "x est-il racine de Q ?"
(par contre, là ou tu me déçoit passablement, c'est que je pensait sincèrement que tu avais un niveau suffisant en math pour savoir qu'avec l'expression générale des solutions d'une équation du second degrés, on avait pas ce type de problème, c'est à dire que l'expression finale x=(-b+-racine(Delta))/(2a) permet bien de répondre à la question "est-ce que x=1 ?" contrairement aux formules de Cardan)
Pour moi, cette écriture, elle est à peu prés du même style que celle consistant à écrire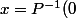) (dans le cas où P est strictement croissante donc bijective) : dans les deux c'est mathématiquement totalement exact, ça donne la valeur exacte de x, mais dans 99% des cas, ça avance à rien vu que ça permet pas d'en déduire quoi que ce soit directement. (quoi que, en fait, je pense que le
(dans le cas où P est strictement croissante donc bijective) : dans les deux c'est mathématiquement totalement exact, ça donne la valeur exacte de x, mais dans 99% des cas, ça avance à rien vu que ça permet pas d'en déduire quoi que ce soit directement. (quoi que, en fait, je pense que le ) est préférable à l'horrible truc de Cardan : ils sont aussi inutile l'un que l'autre, mais le
est préférable à l'horrible truc de Cardan : ils sont aussi inutile l'un que l'autre, mais le ) a au moins le bon gout d'être bien plus court à écrire...
a au moins le bon gout d'être bien plus court à écrire...  )
)
Sinon (bis et répéta), j'attend toujours (patiemment) un malheureux exemple d'exercice où elles auraient un quelconque intérêt.
Pour quelqu'un qui les trouve aussi utile, ça, doit quand même être absolument trivial d'en trouver un, non ?
Je te met le début pour t'aider :
Soit l'unique racine réelle du polynôme
l'unique racine réelle du polynôme =X^3+X+1) .
.
Question 1) Montrer que .... (a toi de continuer)
.... (a toi de continuer)
Indication : on pourra utiliser les formules de Cardan
(contrairement à l'écriture des solution d'une équation du second degré)
Pour faire un peu d'humour, vu que toi, lorsque tu "connait exactement un réel x", ça signifie qu'en fait tu ne sait même pas s'il est égal à 1 (ni s'il est plus grand ou plus petit que 1 d'ailleurs), je me demande ce que ça doit être lorsque tu "ne le connais pas exactement"....

Et, sinon, par exemple (et... par hasard...) il me semble que c'est justement le fait que cette écriture à, on va dire poliment "le mauvais gout" de ne même pas permettre de répondre à la question "est-ce que x=1" qu'il est clair que ça n'a absolument aucun intérêt de la "manipuler" comme tu dit dans un quelconque logiciel de calcul formel (ou encore pire à la main). On aura comme résultat de la "manipulation" un truc du même genre, c'est à dire dont on est complètement incapable de savoir s'il est égal (ou pas) à une autre expression, même si la deuxième expression est aussi simple que "1".
Le premier exemple qui me vient à l'esprit, c'est celui de l'andouille qui, pour savoir si le x en question est racine ou pas d'un second polynôme Q, va "injecter" la formule de cardan dans le second polynôme. Il aura certes une zolie expression finale (d'éventuellement 3 pages...), mais qui aura de nouveau le "mauvais gout" qu'il n'y aura aucun moyen de savoir si l'expression trouvée vaut 0 ou pas (à part évidement en refaisant tout les calculs à l'envers pour remonter aux deux polynômes de départ). Donc de nouveau un truc abominable qui aura pas permis d'avancer d'un millimètre en ce qui concerne la question "x est-il racine de Q ?"
(par contre, là ou tu me déçoit passablement, c'est que je pensait sincèrement que tu avais un niveau suffisant en math pour savoir qu'avec l'expression générale des solutions d'une équation du second degrés, on avait pas ce type de problème, c'est à dire que l'expression finale x=(-b+-racine(Delta))/(2a) permet bien de répondre à la question "est-ce que x=1 ?" contrairement aux formules de Cardan)
Pour moi, cette écriture, elle est à peu prés du même style que celle consistant à écrire
 )
)Sinon (bis et répéta), j'attend toujours (patiemment) un malheureux exemple d'exercice où elles auraient un quelconque intérêt.
Pour quelqu'un qui les trouve aussi utile, ça, doit quand même être absolument trivial d'en trouver un, non ?
Je te met le début pour t'aider :
Soit
Question 1) Montrer que
Indication : on pourra utiliser les formules de Cardan
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: mathématiques seconde
... c'est celui de l'andouille qui, pour savoir si le x en question est racine ou pas d'un second polynôme Q, va ...
Ce n'est pas parce qu'il y a des andouilles qui font n'importe quoi sans réfléchir qu'il faut jeter aux orties l'outil qu'ils sont incapables de manipuler à bon escient.
Il va sans dire (même si pour certaines andouilles, il faut le répéter), que si on a besoin de trouver les racines d'un polynome (3eme ou 4eme degré à coeff réels) on commence par chercher si le polynome n'a pas de racines "évidentes" ou n'est pas d'une forme particulière (ex éq. bicarrée pour 4eme degré) AVANT d'utiliser Cardan ou Ferrari.
Et tu te répètes en t'empêtrant dans tes mauvaises justifications. J'ai dit et répété que j'avais mal lu la question (et cela même en édit dans ma première réponse) et que donc Cardan n'était pas la voie à suivre dans la question initiale spécifique de ce topic.
Toutes tes justifications sur la non utilisation de Cardan ou Ferrari dans le cadre rappelé en rouge ici sont tout simplement
Re: mathématiques seconde
J'attend toujours...Ben314 a écrit:Soitl'unique racine réelle du polynôme
.
Question 1) Montrer que.... (a toi de continuer)
Indication : on pourra utiliser les formules de Cardan
Modifié en dernier par Ben314 le 06 Nov 2016, 10:26, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: mathématiques seconde
J'ai oublié ...
Voila par cardan (en se servant bien entendu d'un "formulaire" comme précisé :
62 secondes montre en main :
Solution réelle de x² + x + 1 = 0

Et si j'en voulais une valeur approchée, je mettrais encore 10 s à l'entrer dans une calculette.
C'est au moins aussi rapide que de monter que la fonction f (de f(x) = x³+x+1) est croissante et à approcher la valeur réelle de x telle que f(x) = 0 par dichotomie au autrement.
Et dans le cas où je voudrais utiliser les résultats (et pas seulement pour x³+x+1 = 0 ... et pas seulement les solutions réelles) de ce type d'équation dans un programme logiciel plus vaste (par exemple qui sort les courbes de phases et de gain dans l'étude de stabilité des servomécanismes), les "formules" de Cardan permettent de le faire très aisément.

Voila par cardan (en se servant bien entendu d'un "formulaire" comme précisé :
62 secondes montre en main :
Solution réelle de x² + x + 1 = 0
Et si j'en voulais une valeur approchée, je mettrais encore 10 s à l'entrer dans une calculette.
C'est au moins aussi rapide que de monter que la fonction f (de f(x) = x³+x+1) est croissante et à approcher la valeur réelle de x telle que f(x) = 0 par dichotomie au autrement.
Et dans le cas où je voudrais utiliser les résultats (et pas seulement pour x³+x+1 = 0 ... et pas seulement les solutions réelles) de ce type d'équation dans un programme logiciel plus vaste (par exemple qui sort les courbes de phases et de gain dans l'étude de stabilité des servomécanismes), les "formules" de Cardan permettent de le faire très aisément.
Re: mathématiques seconde
Bis et répétita : c'est au moins la 10em fois que je te pose exactement la même question à laquelle tu n'as toujours rien répondu
A QUOI CA TE SERT ton écriture x=...
Si c'est pour, comme tu le dit avec tes 10 secondes en plus, avoir un approximation numérique, il est évident que ça va bien plus vite de taper directement un truc du style "fsolve(x^3+x+1)" (sous maple et il y a l'équivalent sur n'importe quel logiciel) que de se faire ch.. à saisir cet énorme truc sans intérêt, non ?
Ca avait du sens à l'époque des tables de log, tables trigo et autres tables de racines carrés et cubique, mais il faudrait peut-être comprendre qu'aujourd'hui, y'a plus grand monde qui utilise des tables...
Et si c'est pas pour avoir une approximation numérique, alors c'est pour quoi ?
A QUOI CA TE SERT ton écriture x=...
Si c'est pour, comme tu le dit avec tes 10 secondes en plus, avoir un approximation numérique, il est évident que ça va bien plus vite de taper directement un truc du style "fsolve(x^3+x+1)" (sous maple et il y a l'équivalent sur n'importe quel logiciel) que de se faire ch.. à saisir cet énorme truc sans intérêt, non ?
Ca avait du sens à l'époque des tables de log, tables trigo et autres tables de racines carrés et cubique, mais il faudrait peut-être comprendre qu'aujourd'hui, y'a plus grand monde qui utilise des tables...
Et si c'est pas pour avoir une approximation numérique, alors c'est pour quoi ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: mathématiques seconde
Et ça, je te l'ai déjà expliqué (mais visiblement tu lit rien du tout), c'est complètement faux :Black Jack a écrit:Et dans le cas où je voudrais utiliser les résultats (et pas seulement pour x³+x+1 = 0 ... et pas seulement les solutions réelles) de ce type d'équation dans un programme logiciel plus vaste (par exemple qui sort les courbes de phases et de gain dans l'étude de stabilité des servomécanismes), les "formules" de Cardan permettent de le faire très aisément.
- Soit le logiciels fait du calcul numérique et il ira aussi vite (voire plus) à calculer directement des approximation des racines du polynômes sans utiliser Cardan et ça permet d'avoir une routine plus générale vu qu'elle permet de chercher les racine de polynôme de degré quelconque.
- Soit ton logiciel fait du calcul formel et là, c'est encore pire vu qu'il va obtenir des résultats formels dont il sera même pas capable de savoir s'ils sont (par exemple) nuls ou pas.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: mathématiques seconde
N'importe quoi, ramasse tes billes et reste avec ta mauvaise fois.
Têtus et sot tu es es et restera.

Têtus et sot tu es es et restera.
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
