Voila après avoir bossé dessus comme une malade à ce devoir, je bloque sur deux questions.
Tout d'abord, voici la figure:
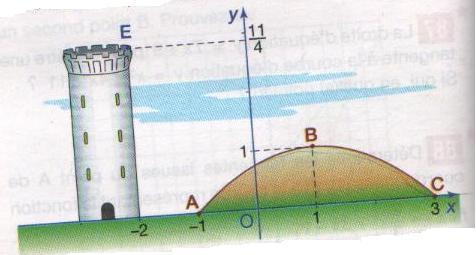
et voici l'énoncé:
Sur la figure ci-contre, "l'arc " de la parabole ABC représente une colline, le sol est symbolisé par l'axe des absisses. Un observateur est placé en E de coordonnées ( -2; 11/4 ) dans le repère choisi.
Le but de l'exercice est de déterminer les points de la colline et ceux du sol qui ne sont pas visibles du point d'observation E.
1. On note f la fonction définie sur [-1;3] par f(x)=ax2+bx+c. Determinez a, b, c pour que "l'arc ABC" soit la représentation grafique de f.
2.a) Reproduisez la figure ci-dessus et indiquez sur la figure les points de la colline et ceux du sol qui ne sont pas visibles de E.
b) Faites les calculs nécessaires pour trouver les absisses de ces points.
Pour la première question, j'ai trouvé une équation égale à y= -1/4x²+1/2x+3/4.
Pour la 2.a), j'ai fait la représentation graphique mais je ne trouve pas le moyen de répondre a la suite de la question. Je sais, d'après quelques recherches quil faut que je calcule l'équation de la tangente passant par le point E et coupant la courbe représentant la colline. Je sais que l'équation d'une tangente est y=f'(a)*(x-a)+f(a). Ainsi je trouve pour f'(a)=> -1/2a+1/2.
Ainsi, pour calculer l'équation, il faut que je développe:
y=(-1/2a+1/2)*(x-a)+(-1/4a²+1/2a+3/4)
Je sais que pour x, je peux remplacer y par l'ordonnée du point E et x par l'abscisse du point E, ce qui me donne:
11/4=(-1/2a+1/2)*(-2-a)+(-1/4a²+1/2+3/4)
Le résultat que je trouve est:
11/4=1/4a²+1/2a-1/4
donc 0=1/4a²+1/2a-12/4
Or lorsque je regarde la "solution" dans d'autres forums, ils ne trouvent pas la même chose que moi. J'ai beau le refaire j'ai l'impression de refaire la même erreur! :hein: :mur: Pourriez vous m'aider?
Pour la question 2.b), je pense avoir une idée mais il faut que je retrouve l'équation de la tangente.
Mais cependant, je ne comprends ce qu'ils veulent dire par "les abscisses de ces points". Ils veulent tous les points ou simplement une intervalle?
Aidez moi s'il vous plaiiiiit!
Merci infiniment!
Sahi
[/CENTER]
