Dm de Mathématiques de 1ere ES : Les suites.

[Melany.C]

Bonjour à tous, j'aurai besoin d'un coup de main pour un Dm de Mathémathique portant sur les suites et dont je n'ai malheureusement pas compris grand chose ... :triste: Dans ce Dm il y a 5 exercices dont 2 que j'ai réussi a éclaircir (enfin je pence ! ) mais les 3 restants sont du chinois pour moi !
Alors voila l'énoncé:


( J'aurai besoin d'aide pour les exercices 2, 3 et 5 qui se ressemble et donc vu que je ne l'ai comprend pas, je ne peux pas les faire.. )

Je vous remercie d'avance!
A bientot!

[flo22]

Bonjour,

prenons l'exercice 2. La première question, as-tu su y répondre ? As-tu appris à te servir de ta calculatrice ?

[Dinozzo13]

Salut et bonnes fêtes :++: !
Exercice 2 :
1.a) Pour compléter ce tableau, tu calcules pour chaque valeurs de n, c'est-à-dire 0,1,2,3 et 4. De même, calcule pour chaque valeur de n du tableau. Or ici, la suite est définie de façon récurrente, c'est-à-dire qu'il un ou plusieurs termes de rang précédent le terme .

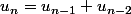
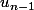
par exemple : , ici la suite est définie de façon récurrente car il y a des termes de rang précédant ceux de ( et ).

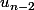
Ici tu as exprimé en fonction de son rang précédent , or on te demande de calculer v_n pour les 5 valeurs de n donc :
Pour , tu regarde ce qui t'es donné dans l'énoncé concernant la suite et tu constate que pour vaut .
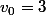
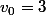
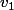
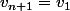
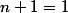
Pour n=1, le "" ne sert que pour donc on en a pas besoin pour le moment puisque . On a donc pas d'autre choix que d'utiliser . Or on veux , il faut donc trouver une valeur de pour laquelle . Ici ce n'est pas très dur, c'est comme résoudre , donc . Ainsi on peut calculer :
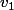
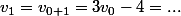
, ok :++: ?
Fais de même avec les 3 autres.
b) Ici, la conjecture est assez évidente :ptdr: .
2.a) Le terme initial de la suite correspond à la première valeur qu'il est possible de prendre pour calculer , ici il s'agit de 0, idem pour .
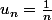
Si l'on avais eu : , le terme initial aurait été car la suite n'est pas définie pour , ok :++: ?
b. C'est que du calcul, l'idée ici est de réécrire 2 comme la différence de deux entiers.
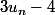
c. Ici, on veut déduire une égalité de terme de la suite entre et , il faut donc exprimer cette égalité en fonction de termes de la suite . Pour cela, tu calcules et examine ce qui se trouve entre parenthèse dans le membre de droite de la relation du b.
d. A partir de la suite définie par récurrence dans l'énoncé, de la conjecture obtenue au 1.b), de 2.a) et 2.c) tu peux en conclure que ... .

Remarque par rapport au 1.a) :
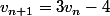
Si tu préfères, est équivalent à .

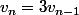
Exercice 3 :
1. Comme pour les fonctions, calcule lorsque vaut , , et .
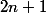
2. Là c'est que de la calculatrice, le problème c'est que j'ai jamais utilisé la calculatrice pour calculer des termes de suites, je ne peux donc pas t'aider pour ça, mais peut-être qu'on en parle dans ton manuel.

Exercice 5 :
1. Ici, je dirai pas besoin de calculatrice, procède comme pour le tableau de l'exercice 1 question 1.a), .
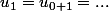
Remarque : Cette question a pour but de te donner une idée de la/les variation de la suite .
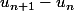
2. Procède simplement, tu devrais calcuer , mais il est donné. Calcule ensuite comme pour l'exercice 4. Puis conclus.

En espérant t'avoir aidé :++: .

[Melany.C]

Oulala dinozzo tu m'as encore plus embrouiller !
:briques:

[Dinozzo13]

Oh :ptdr: .
On peut y aller pas à pas si tu veux :++:

[Melany.C]

Tu as l'air de t'y connaitre ! ;)
La ou j'ai le plus de soucis c'est l'exo 2..
Je ne sais pas comment rédiger les questions 2c et 2d :/
Pourrais-tu me donner un coup de main ?

[Dinozzo13]

Allons-y.
2.c) Ici, il faut savoir d'où on part et à quoi on doit arriver :
On part de ce qui a été fait précédement, c'est-à-dire, et on doit arriver à .
Pour tout n entier naturel : .
Or donc d'où

[Melany.C]

D'accord j'ai compris :)
Et pour la question 2d comment rédigerais-tu ?

[zaze_le_gaz]

et toi tu redigerais comment?

[Melany.C]

Justement le soucis c'est que je ne sais pas comment rédiger..

[zaze_le_gaz]

une phrase simple suffit.