Math équation

[averroes125]

Bonjour à tous,
Quelqu'un pourrait m aider svp pour l'équation ci dessous svp:
Résoudre : x+1/3x+2<=3+x/1-x'

Merci par avance.

[Pisigma]

Bonjour,

c'était déjà mal parti! Ton titre indique "Equation" ; alors que tu veux résoudre une inéquation

de plus, moi je lis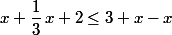 alors que tu ne voulais sûrement pas écrire ça

Donc on attend un énoncé correct!

[Black Jack]

Bonjour,

C'est quasi général dans l'enseignement aujourd'hui ...

On ne connait plus les priorités mathématiques, et non plus l'usage correct des parenthèses.

Je présume qu'il s'agit de : (x+1)/(3x+2) <= (3+x)/(1-x)

(x+1)/(3x+2) - (3+x)/(1-x) <= 0

Et il y a encore probablement une autre erreur d'énoncé ... à corriger avant de poursuivre.

[averroes125]

Merci pour vos réponses, effectivement j ai mal formulé ma demande.

Voila ce que je trouve de mon côte :
(x+1)/(3x+2) <= (3+x)/(1-x')
(x+1)/(3x+2) - (3+x)/(1-x') <= 0
[x-xx'+1-x'-(9x+6+3x²+2x)]/(3x-3xx')+(2-2x')<=0

Le X' me gêne dans cette inéquation, est ce correct avant de poursuivre?

Merci d'avance pour votre aide.

[Pisigma]

je doute de ton x', l'écriture correcte est sûrement celle donnée par Black Jack

il est tiré d'où ton exercice?

[averroes125]

du polycopié partagé par le professeur.

Du coup si erreur du professeur et en refaisant l l'inéquation jusqu'au bout ca donne ca :

(x+1)/(3x+2) <= (3+x)/(1-x)
(x+1)/(3x+2) - (3+x)/(1-x) <= 0
[x-x²+1-x-(9x+6+3x²+2x)]/(3x-3x²)+(2-2x)<=0
(-11x-4x²-5)/-3x²+x+2<=0
Delta = b²-4ac=(-4)²-4*(-11)*(-5) = -204

Merci par avance

[Pisigma]

je te conseille de multiplier le numérateur par -1

il n'est pas nécessaire de développer le numérateur, il vaut mieux garder les 2 facteurs. Ce sera plus facile pour remplir ton tableau de signes

le delta est faux

[Pisigma]

oups!!

il n'est pas nécessaire de développer le dénominateur, il vaut mieux garder les 2 facteurs. Ce sera plus facile pour remplir ton tableau de signes

[averroes125]

merci pour votre réponse, je suis désolé mais je ne vois la subtilité. Pourriez vous m en dire lus svp?

[Pisigma]

tu es arrivé à



je te demande de changer le signe du numérateur

ensuite il faut écrire le numérateur sous la forme d'un produit de facteurs et faire un tableau de signes pour résoudre ton inéquation

[averroes125]

si j ai bien compris :

(4x²+11x+5x)/(-3x-2)(-1+x)<=0
Delta = b²-4ac= 11²-4x4x5=41
X1=(-b-Racine carré Delta)/2a= (-11-Racine carré 41)/8=-2.2
X2 =-0.6

Merci par avance

[Pisigma]

Il suffisait d'écrire



sans changer le dénominateur

[averroes125]

Effectivement.
Merci de m avoir accordé du temps.

[Pisigma]

de rien