Math - Equation différentiel

[Liam20]

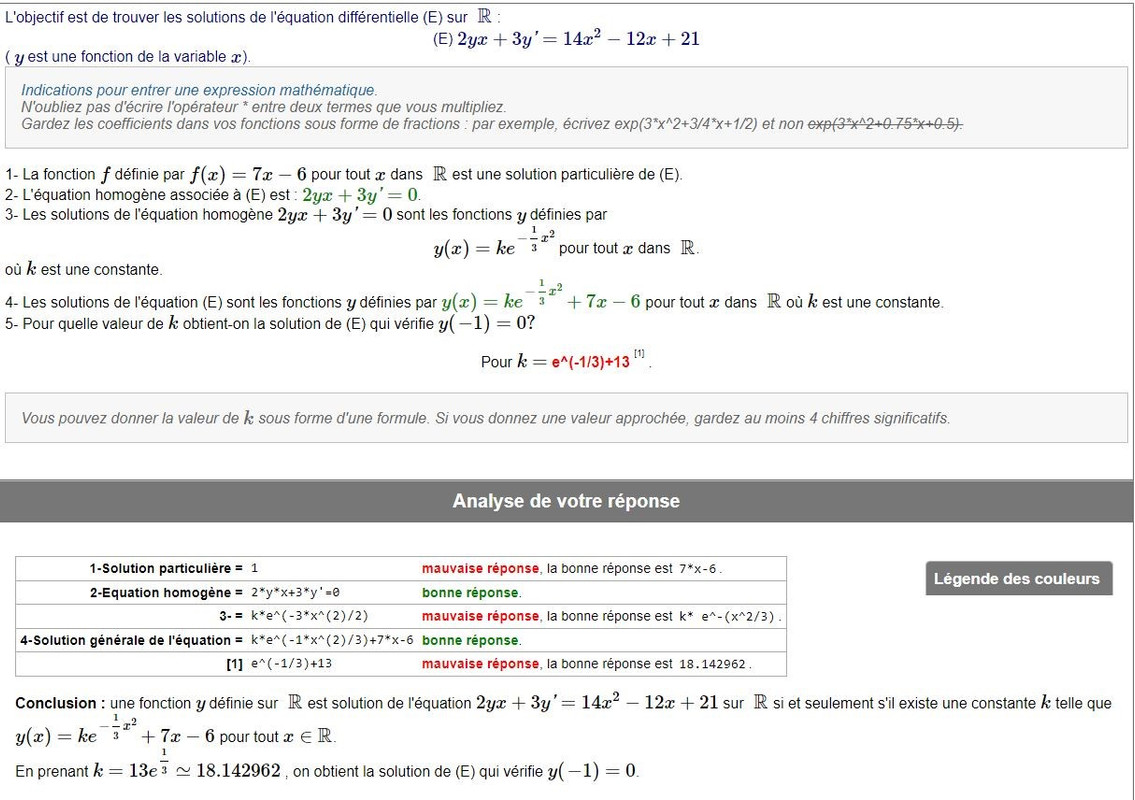
Bonjour pouvez vous m'aider faire démonstartion sur cette exercice parce que je sais trouver la solution avec Eq.diff normale mais lorsque il y a (x ou t) devant y comme exercice ci dessous je suis bloqué je ne sais pas comment faire , j'ai essayé mais toujours fausse vous pouvez voir dans la photo sur le partie pour trouver (la fonction f définit par f(x) ???? je suis bloqué dans ce point là)

Photo exercice :

[Liam20]

[Vassillia]

Bonjour,

Pour résoudre l'étape 1, il faut trouver une solution particulière c'est à dire une solution (n'importe laquelle) qui vérifie (E)
Ici tu as comme indice que cette fonction est de la forme
La première chose à faire est de dériver puis de remplacer y et y' par et dans l'équation, ainsi tu devrai avoir une égalité qui te permet de trouver a, b et c en identifiant les coefficients.

[Liam20]

Merci j'essaie refaire ça

[Liam20]

désolé j'ai encore question , le problème c'est de trouver la dériver je suis bloqué quand je pose f'(t) parce que il y (x ou t) comme ça devant y' donc ça me bloque.

par exemple je prends comme cela y' +y = 2x +1 pour résoudre la fonction f(x) tout d'abord je fais :

yp =ax +b

y'p = a

Je remplace dans (E) : y' +y = 2x +1 :

a + ax+ b = 2x+1

l'étape suivant on réoudre Equation :

a = 2
a + b = 1
---------------------
a = 2
2+b = 1
---------------------
a = 2
b = -1

[Vassillia]

Bonjour,

J'ai un petit peu de mal à comprendre ce que vous faites, il me semblait que l'objectif était de résoudre
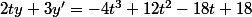
On a donc
En remplacant dans l'équation (E), on obtient
On développe l'expression
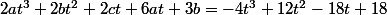
Il reste à trouver les valeurs de a, b et c pour que l'égalité soit vraie

[Liam20]

Merci beaucoup, avant j'étais mal devéloppé avec 2t(at^2+bt+c) mais maintenant j'ai compris

2a = -4
2b = 12
2c+6a = -18

-------------------------------
a= -2
b = 6
c= -3

Merci encore