Manipulation de puissances
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 09 Fév 2013, 12:20
par Dante0 » 09 Fév 2013, 12:20
Bonjour,
Peut-on m'expliquer comment on passe de :
^{\frac{-1}{2}}\times q1^{\frac{-1}{6}}= p2)
à
^{\frac{1}{2}} \times \frac{1}{p2})
Merci!
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 09 Fév 2013, 12:21
par XENSECP » 09 Fév 2013, 12:21
Il manque un "=" dans la première expression.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 09 Fév 2013, 12:23
par XENSECP » 09 Fév 2013, 12:23
Tu passe le
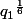
de l'autre côté et tu passes
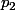
de l'autre.
Pour la fraction, tu l'inverse pour changer le signe de la puissance.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 10 Fév 2013, 08:48
par Dante0 » 10 Fév 2013, 08:48
XENSECP a écrit:Tu passe le
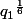
de l'autre côté et tu passes
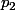
de l'autre.
Pour la fraction, tu l'inverse pour changer le signe de la puissance.
En gros y'a une règle qui dit que :
^{-2} = (\frac{y}{x})^{2})
?
Et donc si
^{-2} = z)
alors
^{2} = \frac{1}{z})
?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 10 Fév 2013, 10:03
par Kikoo <3 Bieber » 10 Fév 2013, 10:03
Salut,
Dante0 a écrit:En gros y'a une règle qui dit que :
^{-2} = (\frac{y}{x})^{2})
?
Et donc si
^{-2} = z)
alors
^{2} = \frac{1}{z})
?
Oui oui, l'exposant -1 est lié à l'inversion.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 10 Fév 2013, 10:42
par Dante0 » 10 Fév 2013, 10:42
Après l'entrée voila le plat de résistance...
On a un système :
^{\beta}<br />\end{array}<br />\right.)
^{\frac{\beta}{\alpha + \beta}}<br />\end{array}<br />\right.)
La ou il y'a les ... je suis censé trouver la valeur de q2 qui doit etre égale à
^{\frac{\beta}{\alpha + \beta}})
en remplacant par q1
Comment faire ce calcul je m'embrouille à fond dans les puissances... :mur:
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 11 Fév 2013, 15:05
par Dante0 » 11 Fév 2013, 15:05
Up svp ! :hein:

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 11 Fév 2013, 15:16
par ampholyte » 11 Fév 2013, 15:16
Bonjour,
Il te suffit simplement d'injecter q1 dans q2:
^{\frac{\beta}{\alpha + \beta}})
Tu peux déjà réorganiser ton expression.
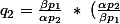^{\frac{\beta}{\alpha + \beta}} \ * \ q^{\frac{1}{\alpha+\beta}})
Ensuite tu peux écrire
^{-1} = \frac{\beta p_1}{\alpha p_2})
Donc
^{-1} \ * \ (\frac{\alpha p_2}{\beta p_1})^{\frac{\beta}{\alpha + \beta}} \ * \ q^{\frac{1}{\alpha+\beta}})
Là tu as une forme
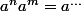
Je te laisse continuer

-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 14 Fév 2013, 23:01
par Dante0 » 14 Fév 2013, 23:01
ampholyte a écrit:Bonjour,
Il te suffit simplement d'injecter q1 dans q2:
^{\frac{\beta}{\alpha + \beta}})
Tu peux déjà réorganiser ton expression.
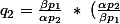^{\frac{\beta}{\alpha + \beta}} \ * \ q^{\frac{1}{\alpha+\beta}})
Ensuite tu peux écrire
^{-1} = \frac{\beta p_1}{\alpha p_2})
Donc
^{-1} \ * \ (\frac{\alpha p_2}{\beta p_1})^{\frac{\beta}{\alpha + \beta}} \ * \ q^{\frac{1}{\alpha+\beta}})
Là tu as une forme
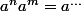
Je te laisse continuer

On peut simplifier comme suit
^{\frac{-\alpha}{\alpha + \beta}} \ * \ q^{\frac{1}{\alpha+\beta}})
mais ensuite ?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 15 Fév 2013, 09:15
par ampholyte » 15 Fév 2013, 09:15
Tu cherches à trouver cette forme :
^{\frac{\beta}{\alpha + \beta}})
N'oublie pas que
^{-1})
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 15 Fév 2013, 09:31
par Dante0 » 15 Fév 2013, 09:31
ampholyte a écrit:Tu cherches à trouver cette forme :
^{\frac{\beta}{\alpha + \beta}})
N'oublie pas que
^{-1})
C'est ce que je viens de faire non ?
En classe on a marqué
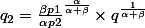
ce qui équivaut à ce que j'ai trouvé dans mon précédent message non ?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 15 Fév 2013, 09:56
par ampholyte » 15 Fév 2013, 09:56
Oui désolé, j'avais mal vu la forme de ta solution. Tu as donc trouvé q2 !
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 15 Fév 2013, 19:27
par Dante0 » 15 Fév 2013, 19:27
Ok

Après on admet une fonction telle que
 = p1q1+p2q2)
 = [p1\times (\frac{\alpha p_2}{\beta p_1})^{\frac{\beta}{\alpha + \beta}} + p2\times(\frac{\beta p1}{\alpha p2}^{\frac{\alpha}{\alpha +\beta}}]\times q^{\frac{1}{\alpha+\beta}})
 = [(\frac{\alpha}{\beta})^{\frac{\beta}{\alpha +\beta}} + (\frac{\beta}{\alpha})^{\frac{\alpha}{\alpha +\beta}}]\times p1^{\frac{\alpha}{\alpha +\beta}}\times p2^{\frac{\beta}{\alpha +\beta}}\times q^{\frac{1}{\alpha +\beta}})
Je ne comprends pas comment on passe à la dernière étape.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 16 Fév 2013, 17:07
par Dante0 » 16 Fév 2013, 17:07
:help: :help:

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 17 Fév 2013, 15:19
par ampholyte » 17 Fév 2013, 15:19
Tu peux par exemple utiliser le fait que
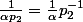
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 17 Fév 2013, 16:56
par Dante0 » 17 Fév 2013, 16:56
ampholyte a écrit:Tu peux par exemple utiliser le fait que
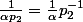
Ca ne m'aide pas trop :s
Il y'a pas mal de truc que je comprends pas, comment p1 et p2 sont affectés de leurs exposants, comment on a factorisé.... parce que pour moi la première forme n'est pas simplifiable.

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 17 Fév 2013, 20:51
par ampholyte » 17 Fév 2013, 20:51
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 19 Fév 2013, 13:29
par Dante0 » 19 Fév 2013, 13:29
Merci pour l'effort !!
T'as oublié d'enlever le p1 à la 3e ligne non ?
Comment tu développes la dernière expression sinon ?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 19 Fév 2013, 13:34
par ampholyte » 19 Fév 2013, 13:34
Pas de quoi !
J'ai corrigé la coquille à la 3eme ligne (je ne l'ai pas vu à la relecture)
Concernant le développement de la dernière expression, on obtient tout simplement :
 = (\frac{\alpha}{\beta})^{\frac{\beta}{\alpha + \beta}} \times {p_2}^{\frac{\beta}{\alpha + \beta}} \times {p_1}^{\frac{\alpha}{\alpha +\beta}}\times q^{\frac{1}{\alpha+\beta}} +(\frac{\beta}{\alpha })^{\frac{\alpha}{\alpha +\beta}} \times {p_1}^{\frac{\alpha}{\alpha +\beta}} \times {p_2}^{\frac{\beta}{\alpha +\beta}}\times q^{\frac{1}{\alpha+\beta}})
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 19 Fév 2013, 17:26
par Dante0 » 19 Fév 2013, 17:26
ampholyte a écrit:Pas de quoi !
J'ai corrigé la coquille à la 3eme ligne (je ne l'ai pas vu à la relecture)
Concernant le développement de la dernière expression, on obtient tout simplement :
 = (\frac{\alpha}{\beta})^{\frac{\beta}{\alpha + \beta}} \times {p_2}^{\frac{\beta}{\alpha + \beta}} \times {p_1}^{\frac{\alpha}{\alpha +\beta}}\times q^{\frac{1}{\alpha+\beta}} +(\frac{\beta}{\alpha })^{\frac{\alpha}{\alpha +\beta}} \times {p_1}^{\frac{\alpha}{\alpha +\beta}} \times {p_2}^{\frac{\beta}{\alpha +\beta}}\times q^{\frac{1}{\alpha+\beta}})
Ok génial merci pour ton intervention très efficace !

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités