Manipulation de fonctions numériques

[mateus]

Bonjour à tous et toutes, je ne suis plus étudiant mais durant mes études j'avais des difficultés en mathématique et je souhaite aujourd'hui m'améliorer en m’exerçant, j'ai trouvé un sujet sur internet (bien qu'il soit en anglais désolé pour ceux qui ne sont pas à l'aise avec l'anglais) lequel j'ai du mal à comprendre la solution pourtant il ne paraît pas extrêmement compliqué. Vous pouvez trouver le sujet en attachement.

Je ne comprends pas déjà cette phrase : "dont la valeur en r est égal à la somme des valeurs des deux fonctions numériques en r."

Ensuite la seule chose que je comprends dans la solution c'est le 3^-r + 12 qui est égal à 3^-r+7 + r + 5 mais le reste des lignes je ne comprends pas quelqu'un pourrait-il m'expliquer ?

Merci par avance.

Mathieu

[Pseuda]

Bonjour,

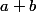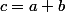C'est très simple. Cela dit simplement que si et sont deux fonctions numériques de réel, alors la fonction définie par est aussi une fonction numérique de . On peut l'appeler , et on peut aussi écrire sous forme indicielle . Idem pour le produit.

ici, est un entier, mais c'est pareil.

[mateus]

Merci beaucoup Pseuda pour ta réponse mais je t'avoue que je ne comprends toujours pas la solution avec ta réponse

[Black Jack]

Je montre en faisant l'exercice pour la somme ... avec un vocabulaire auquel on est plus habitué.

Soit 2 fonctions numériques f et g telles que :

f(x) = 0 pour 0 <= x <= 3
f(x) = 3^(-x) + 7 si x >= 4

et
g(x) = 3-2^x pour 0 <= x <= 2
g(x) = x + 5 pour x >= 3

Obtenir h = f + g
-----

Le domaine d'existence de h est l'intersection des domaines d'existence de f et g -->
(donc h n'existe que pour les valeurs de x telles que f et g existent toutes les deux)

---> h existe pour 0 <= x <= 2 UNION x = 3 UNION x >= 4

a)
Pour 0 <= x <= 2 : f(x) = 0 et g(x) = 3-2^x
h(x) = f(x) + g(x) = 0 + 3-2^x = 3 - 2^x

b)
Pour x = 3 : f(x) = f(3) = 0 et g(x) et g(3) = x+5 = 3+5 = 8
h(x) = f(x) + h(x) = 0 + 8 = 8

c)
Pour x >= 4 : f(x) = 3^(-x) + 7 et g(x) = x + 5
h(x) = f(x) + g(x) = 3^(-x) + 7 + x + 5 = 3^(-x) + x + 12


Et donc finalement :

la fonction h = f+g est telle que :

h(x) = 3-2^x pour 0 <= x <= 3
h(x) = 8 pour x = 3
h(x) = 3^(-x) + x + 12 pour x >= 4

[Pseuda]

Les fonctions a et b sont définies sur N (ensemble des entiers positifs), avec des expressions différentes selon la valeur de la variable r.

Donc on cherche des intervalles de définitions communs aux 2 fonctions dans lesquels les expressions de a et b ne changent pas. Par exemple on distingue , , etc.. .
Pour , c'est-à-dire pour r=0, 1 ou 2, et , donc .
Pareil pour les autres sous-ensembles.

[mateus]

Merci pour vos réponses j'ai mieux compris, c'est gentil, là où j'ai vraiment du mal avec les maths c'est comprendre ce qui est vraiment demandé dans un problème posé et ça a toujours été mon problème, dès que cela devient abstrait c'est fini, je me perds, quand c'est du calcul numérique ou des raisonnements non abstraits ça va mais sinon... Ce que je n'arrive pas à comprendre c'est que si Black Jack et vous même Pseuda n'auriez pas détaillé le problème je n'aurai pas pu comprendre, même si je serai passé 2 semaines sur le pb. C'est ça que je trouve dommage dans les mathématiques... J'essaie de trouver une solution pour m'améliorer mais je sais pas s'il en existe une vraiment, peut-être faut t-il avoir un sens particulier, une manière bien différente de penser les choses, j'ai fais beaucoup de recherches à ce sujet et j'avoue que c'est assez vague, personne n'arrive à se mettre d'accord sur l'incompréhension des abstractions mathématiques de certaines, certains (comme moi même). Bien le merci à vous et bonne journée. Mathieu