Majoration d'une suite

[Pseuda]

Bonjour,

Un doute m'assaille : dans un livre de TS au détour d'une question : montrer que pour tout .

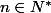
Comment le montrer avec les moyens du lycée (on ne connaît pas la formule du binôme de newton, la croissance de la suite et sa convergence vers e, les DL, ...)?

[Ben314]

Salut,
Il y a éventuellement une astuce (que je ne vois pas...), mais sinon, si on connait les exp et les log alors

puis l'étude des variations de permet de montrer facilement que pour tout et on en déduit que pour tout entier n.

[Pseuda]

Merci, cela m'est venu en te lisant. C'est un exercice sur la fonction exponentielle, ils ne connaissent pas encore les logarithmes, mais je pense qu'on est supposé connaître la valeur de e 2,718, et on a montré avant que pour tout n.

Si on y réfléchit bien, cela se mord la queue, mais bon.